No It cannot be done. Each rectangle covers one white square and one black square, because on a chess board the white and black squares are always adjacent…..The two squares which we remove from the chess board are of the same colour, and so the remaining board has two more boxes of one colour than the other. And after the rectangles have covered 60 boxes, there will be left two squares of the same colour.

Obviously the remaining rectangle cannot cover these two squares.

There were 991 cats, and each of them killed 1009 mice.

Get the prime factorization of 999919
The prime factors are 991 and 1009 only

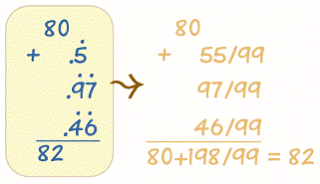
The dot over a number signifies that it is a repeater which would go on for ever, as when we endeavor to describe 1/3 decimally as 0.33333 . . . . (etc)
With a series of numbers we place the dot over the first and last, as with 0.97979797979 . . . (etc)
The remarkable feature being that a proper fraction divided by 9s e.g. 46/99 is exactly equal to the numerator with the repeater sign followed by the decimal.

Total 7 races are required –
__________________________________________________________________________
We will have 5 races with all 25 horses
Let the results be
a1,a2,a3,a4,a5
b1,b2,b3,b4,b5
c1,c2,c3,c4,c5
d1,d2,d3,d4,d5
e1,e2,e3,e4,e5

Where a1 faster than a2 , a2 faster than a3 etc and We need to consider only the following set of horses
a1,a2,a3,
b1,b2,b3,
c1,c2,c3,
d1,d2,d3,
e1,e2,e3,

Race 6
We race a1,b1,c1,d1 abd e1
Let speed(a1)>speed(b1)>speed(c1)>speed(d1)>speed(e1)

We get a1 as the fastest horse, We can ignore d1,d2,d3,e1,e2 and e3

a2,a3,
b1,b2,b3,
c1,c2,c3,

Race 7

Race a2,a3,b1,b2 and c1
The first and second will be second and third of the whole set

The obvious answer is that the police did not tell him where the wife was murdered but he reached the site.

Lunch 😛 😛

Dinner 😛

16 cups tea (about half of pot A).
The amount of tea that can be kept within each pot is determined by the height of the spout opening. The tea level cannot rise above the spout opening since any extra tea would merely spill out from the spout.
Visual estimate would conclude that the spout of teapot B is approximately half the height of that of teapot A, therefore providing only half of the capacity, or 16 cups tea.

Sage A’s hat is white.
It cannot be blue.

1. The puzzle says that “Sage A sees that the other 2 sages are wearing blue hats.” So both sage B and sage C wear blue hats. That’s a given.

2. Neither B or C can deduce the color of their own hats, and therefore, they remain silent.

Here’s why:
If A’s hat were white, B would see C’s blue hat, and see A’s white hat. B’s hat could be either blue or white.

If A’s hat were blue, B would see C’s blue hat, and A’s blue hat. B’s hat could still be either blue or white.

If A’s hat were white, C now would see B’s blue hat, and see A’s white hat. C’s hat could be either blue or white.

If A’s hat were blue, C would see B’s blue hat, and see A’s blue hat. C’s hat could still be either blue or white.

So Sage B and C cannot speak up for sure.

3. After a while, when Sage A sees that neither sage B or sage C speak up, (and they speak up if they could solve the ridde), sage A reasons that neither sage B nor sage C, based on what they see, can deduce the color of their own hats.

Sage A reasons further that since one of the three sages should be able to speak to the king, sage A alone must be the one able to figure it out, since the other two cannot.

There must be something that makes him unique, something that he sees that the other two don’t see, something that he sees that makes the riddle solveable for him, while the other two cannot solve it. What does he see?
He sees two blue hats (B’s blue hat and C’s blue hat). So Sage A again reasons correctly that only he sees two blue hats. Since sage B’s hat is blue and sage C’s hat is blue, Sage A correctly reasons that his own hat cannot be blue. (Or else all three sages would see the other two sages wear blue hats).

So A’s hat must be white, and so A speaks up.

————————-

Note:
If A’s hat were blue, all three sages would be wearing blue, each sage would see the other two wearing blue hats, and there would be nothing to differentiate them, with all three silent. Nobody would speak up and they would all go home.

10.
Alternate solution-
Number the bottles, write that in binary, number prisoners from 1 to 10. Prisoner i drinks bottle n if bit i of n is 1. Each dead prisoner tells you that bit i of poisoned bottle is 1.