The famous Monty Hall Problem
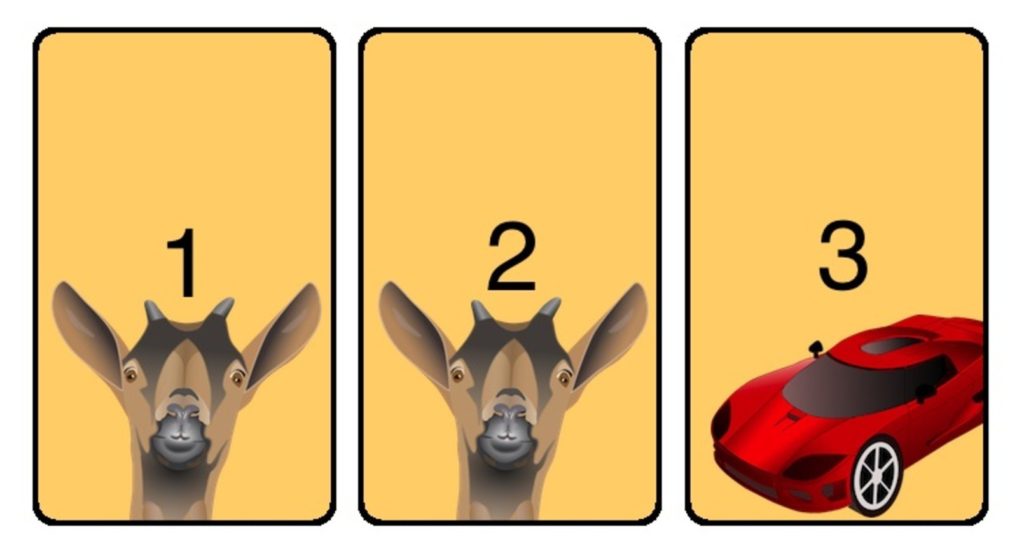
You’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?
With you switch or stay with your door?
SWITCHING will be more advantageous,
Switching will make winning probability to 2/3 and staying will have probability 1/3
_______________________________________________________________________________________
Assume that you always start by picking Door #1, and the host then always shows you some other door which does not contain the car, and you then always switch to the remaining door.If the car is behind Door #1, then after you pick Door #1, the host will open another door (either #2 or #3), and you will then switch to the remaining door (either #3 or #2), thus LOSING.
If the car is behind Door #2, then after you pick Door #1, the host will be forced to open Door #3, and you will then switch to Door #2, thus WINNING.
If the car is behind Door #3, then after you pick Door #1, the host will be forced to open Door #2, and you will then switch to Door #3, thus WINNING.
Hence, in 2 of the 3 (equally-likely) possibilities, you will win. Ergo, the probability of winning by switching is 2/3.
Choose an explanation to the Monty Hall Problem:
1/3 vs 2/3 – Solution #1 to the Monty Hall Problem
There is a 1/3 chance of the car being behind door number 1 and a 2/3 chance that the car isn’t behind door number 1. After Monty Hall opens door number 2 to reveal a goat, there’s still a 1/3 chance that the car is behind door number 1 and a 2/3 chance that the car isn’t behind door number 1. A 2/3 chance that the car isn’t behind door number 1 is a 2/3 chance that the car is behind door number 3.
100 Doors! – Solution #2 to the Monty Hall Problem
Imagine that instead of 3 doors, there are 100. All of them have goats except one, which has the car. You choose a door, say, door number 23. At this point, Monty Hall opens all of the other doors except one and gives you the offer to switch to the other door. Would you switch? Now you may arrogantly think, “Well, maybe I actually picked the correct door on my first guess.” But what’s the probability that that happened? 1/100. There’s a 99% chance that the car isn’t behind the door that you picked. And if it’s not behind the door that you picked, it must be behind the last door that Monty left for you. In other words, Monty has helped you by leaving one door for you to switch to, that has a 99% chance of having the car behind it. So in this case, if you were to switch, you would have a 99% chance of winning the car.
Pick a Goat – Solution #3 to the Monty Hall Problem
To win using the stay strategy, you need to choose the car on your first pick because you’re planning to stay with your initial choice. The chance of picking the car on your first pick is clearly one out of three. But, in order to win using the switch strategy, you only need to pick a goat on your first pick because the host will reveal the other goat and you’ll end up switching to the car. So you want to use the strategy that lets you win if you choose a goat initially because you’re twice as likely to start by picking a goat.
Scenarios – Solution #4 to the Monty Hall Problem
To understand why it’s better to switch doors, let’s play out a few scenarios. Let’s see what will happen if you were to always stay with your original choice. We’ll play out three scenarios, one for each door that the car could be behind (door number 1, door number 2, or door number 3). And it doesn’t matter which door you start out with, so, to keep it simple, we’ll always start by choosing door number 1.Stay strategy, scenario 1: the car is behind door number 1. You choose door number 1, then the host reveals a goat behind door number 2 and because you always stay, you stay with door number 1. You win the car! Stay strategy, scenario 2: the car is behind door number 2. You start by picking door number 1, the host reveals a goat behind door number 3, and you’re using the stay strategy so you stay with door number 1. You get a goat and don’t win the car. Stay strategy, scenario 3: the car is behind door number 3. You pick door number 1, the host opens door number 2 to reveal a goat, you stay with door number 1, and you get a goat. So, using the stay strategy, you won the car one out of three times. That means that in any one instance of playing the game, your chance of winning the car if you choose to stay is 1/3 or about 33%.
Now let’s try switching doors. Again, we’ll always start by picking door number 1. Switch strategy, scenario 1: the car is behind door number 1. You choose door number 1, the host opens door number 2 to reveal a goat, you are using the switch strategy so you switch to door number 3. You get a goat. Switch strategy, scenario 2: the car is behind door number 2. You start by picking door number 1, the host opens door number 3 to reveal a goat, you switch to door number 2 and win the car! Switch strategy, scenario 3: the car is behind door number 3. You pick door number 1, the host opens door number 2 to reveal a goat, you switch to door number 3 and win the car again! So, with the switch strategy you won the car 2 out of 3 times. That means, that in any one instance of the game, your chance of winning the car if you choose to switch doors is 2/3 or about 67%.
Therefore, if you play the game three times and stay, on average you’ll win the car once. But if you play the game three times and switch each time, on average you’ll win the car twice. That’s twice as many cars!
Your Answer
More puzzles to try-

How much money did he have to begin with?
A man spends one fifth of the money in his wallet. He then spends one fifth of what remains in ...Read More »
No lungs to breathe
I have no legs to dance and no lungs to breathe, No life to live or die, but yet I ...Read More »
Date on Dice
There are two dice with empty faces in front of you and a marker. You can mark any number on ...Read More »
Solve the EST EST EST EST rebus riddle
Treasure is present in a place represented in the rebus, Solve the rebus riddle? What place is it? EST EST ...Read More »
Have Bank but No Money
I have a mouth but I don\’t eat. I have a bank but have no money. I have a bed ...Read More »
Find the number
Double it and multiply it by 4. Then divide it by 8 and you’ll have it once more. What number ...Read More »
Ninety One Riddle
Below equation is true. 8 + 8 = 91 How ?Read More »
Tuesday, Thursday what are other two days staring with T?
Four days are there which start with the letter ‘T‘. I can remember only two of them as “Tuesday , Thursday”. ...Read More »
Logical Number in Center
What number should come in place of the question mark below?Read More »
Solve this number puzzle

Good to eat
I walked through a field of wheat, I picked up something good to eat, It was white and had no ...Read More »
Rescue! The Frog
A frog is at the bottom of a 30 meter well. Each day he summons enough energy for one 3 ...Read More »
Fins and Feathers
Hostile members of the Uti, Grundi and Yomi groups were travelling to a conference. There were two members from each ...Read More »
One Quarter riddle
What number is one half of one third of one quarter of 360?Read More »
Question in probability exam What is risk puzzle
There was once a college that offered a class on probability applied to the real world.The class was relatively easy, ...Read More »
Wears cap without head
What wears a cap, but has no head?Read More »
Can You?
I make babies look smart, I make you look dumb, I make your phone work, I stop you from freezing ...Read More »
Rats step back
What would you get if 100 rats took one step backwards at the same time?Read More »
How long would it take?
To dye a single Easter egg takes 7.5 minutes if you leave it in dye. How long would it take ...Read More »
The Barbershop and traveler Puzzle
A traveler arrives in a small town and decides he wants to get a haircut. There are only two barbershops ...Read More »


