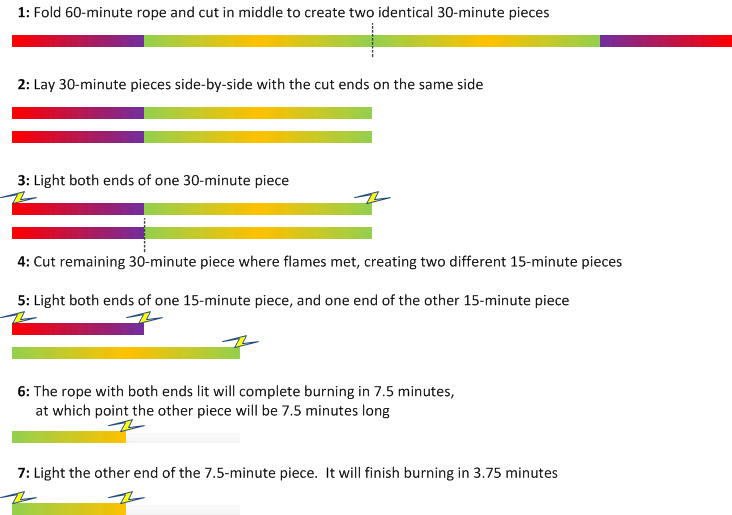487
points
Questions
1
Answers
36
-
This answer accepted by SherlockHolmes. on 6th June 2016 Earned 20 points.
- 4217 views
- 2 answers
- 1 votes
-
Where n > 1, if you cut a painted n-inch cube into 1-inch cubes, you will have:
n^0: 8 * n^0 cubes with 3 sides painted
n^1: 12 * (n – 2)^1 cubes with 2 sides painted
n^2: 6 * (n – 2)^2 cubes with 1 side painted
n^3: (n – 2)^3 cubes with 0 sides paintedSo plugging in 4 for n gives:
8 * 4^0 = 8 * 1 = 8 cubes with 3 sides painted
12 * (4-2)^1 = 12 * 2^1 = 12 * 2 = 24 cubes with two sides painted
6 * (4-2)^2 = 6 * 2^2 = 6 * 4 = 24 cubes with one side painted
(4-2)^3 = 2^3 = 8 cubes with no side painted- 6574 views
- 3 answers
- 0 votes
-
2 hours and 12 minutes.
This question can actually be answered with less information–it’s not necessary to know how far ahead the minute hand is, only how much further ahead it is the second time. So this answer considers the question to be:
An observation is made on a clock and it is found that the hour hand is placed exactly at the minute mark. After some time, the clock is observed again and it is found that the hour hand is exactly on another minute mark while the minute hand is one minute further ahead of the hour hand than the minute hand was ahead of the hour hand when the first observation was made.
Every 12 minutes, or five times an hour, the hour hand is exactly on a minute mark. Every 12 minutes, the minute hand advances 12 minutes and the hour hand advances one minute, so the distance between the hour and minute hand increases by 11, modulo 60.
If the number of 12-minute periods that pass is p, then we want to solve for 11p modulo 60 = 1. So starting with 1, keep adding 60 until we find the first multiple of 11:
1, 61, 121 <– BINGO
121 = 11 * 11, so the minimum number of 12 minute periods that have passed is p = 11. 11 * 12 = 132 minutes = 2 hours and 12 minutes.
—
Since 11 and 60 are relatively prime, we know that in a 12 hour period, the hour hand will be on a minute mark 60 different times and the amount the minute hand is ahead of the hour hand will be different on each occasion, with the difference assuming each of the values from 0 to 59. This realization is what allows the problem to be uniquely solved with only the information about how much the difference between the hour and minute hand changed.
This answer accepted by SherlockHolmes. on 9th November 2015 Earned 20 points.
- 4550 views
- 2 answers
- 2 votes
-
3 69258/714
81 5643/297
81 7524/396
82 3546/197
91 5742/638
91 5823/647
91 7524/836
94 1578/263
96 1428/357
96 1752/438
96 2148/537I found these without writing a program.
The mixed fraction i n/d has integer portion i , numerator n , and denominator d. The integer portion i must have one or two digits, giving two possible partitions of the nine digits into i, n & d, with 9! = 362,880 ways to arrange the nine digits in each, giving a total initial search space of 725,760 arrangements for i, n & d:
- If i is a single digit (i1), then n must be five digits (n1, n2, n3, n4, n5) and d three digits (d1, d2, d3) such that 91 <= n/d <= 99. The range of possible values for n/d are 12345/987 = 12 to 98765/123 = 802. The maximum value for n/d when the first digit of n is 1 is 19876/234 = 84, so the first digit of n can’t be 1. The minimum value for n/d when the first digit of n is 9 is 91234/876 = 104, so the first digit of n also can’t be 9. Since the first digit of n can’t be 1 or 9, there are only 7 * 8! = 282,240 possible permutations with a one-digit i
- If i is two digits (i1, i2), then n must be four digits (n1, n2, n3, n4) and d three digits (d1, d2, d3). The range of possible values for n/d are 1234/987 = 1 to 9876/123 = 80. Since i can’t be 99, the effective minimum is 2; since i2 can’t be zero, the effective maximum value is 79. This give 21 <= i <= 98. Since i1 can’t be 1, there are only 8 * 8! = 322,560 possible combinations with a two-digit i.
Now the search space is 282,240 + 322,560 = 604,800, which is a 17% reduction.
There are 9 * 8 * 7 = 504 combinations for the final digit of i, n and d (dfi, dfn, and dfd respectively) where each digit is a different value from 1 to 9. However, only 36 combinations satisfy the requirement that the final digit of (10 – dfi) * dfd = dfn. The possible combinations for (dfi, dfn, dfd ) are:
(1,2,8) (1,3,7) (1,4,6) (1,6,4) (1,7,3) (1,8,2)
(2,4,3) (2,4,8) (2,6,7) (2,8,1) (2,8,6)
(3,2,6) (3,4,2) (3,6,8) (3,7,1) (3,8,4) (3,9,7)
(4,2,7) (4,6,1) (4,8,3)
(6,2,3) (6,2,8) (6,4,1) (6,8,2) (6,8,7)
(7,2,4) (7,3,1) (7,4,8) (7,6,2) (7,8,6) (7,9,3)
(8,2,1) (8,2,6) (8,4,2) (8,4,7) (8,6,3)It’s worth noting that no final digit can be 5 and neither dfi nor dfd may be 9 and dfi can’t be 1. This means for single-digit i that 92 <= n/d <= 99.
None of those combinations has both a 1 and a 9. 12 combinations have a 1, and 2 combinations contain a 9.
- For single-digit i there are 5 * 5! = 600 ways to assign the remaining 6 digits for the 12 + 2 = 14 combinations that contain a 1 or 9; there are 4 * 5! = 480 ways to assign the remaining digits for the 36 – 14 = 22 combinations that don’t contain a 1 or 9. The search space for single-digit i is now 600 * 14 + 480 * 22 = 18,960.
- For two-digit i there are 6! = 720 ways to assign the remaining 6 digits for the 12 combinations that contain a 1; there are 5 * 5! = 600 ways to assign the remaining digits for the 36 – 12 = 24 combinations that don’t contain a 1. The search space for two-digit i is now 720 * 12 + 600 * 24 = 23,040.
Now the search space is 18,960 + 23,040 = 42,000, which is a 94% reduction from the initial search space.
From here, we can continue to prune the search space by cases that fix the assignment of one or more digits. Eventually, it comes down to checking the remaining possible permutations. For single-digit i, the most useful digit to assign first is the most-significant digit of n, which is already limited to 2..8. For two-digit i, the most useful digit to fix is the most-significant digit of i, which is already limited to 2..9. For those interested, the following discussion prunes down the possible values further. All division uses the floor value (rounding down) for maximum values or ceiling value (rounding up) for minimum values.
Single-digit i, cases for n1:
2: For 21346 <= n <= 29876, the range of values for d are 21346/99 = 216 to 29876/92 = 324. However, if n1 = 2, then d1 can’t be 2 and must be 3. This gives 314 <= d <= 318 (since d2 can’t be 2 and dfd can’t be 9) making d2 = 1, and making the minimum value for n = 92 * 314 = 28888. 1, 2 & 3 are assigned, and n2 must be 8 or 9. There are only four combinations for dfi, dfn, and dfd that don’t have a 1, 2 or 3: (6,8,7), (7,4,8), (7,8,6) and (8,4,7). Each of those has an 8, making n2 = 9. For each of the four combinations for dfi, dfn, and dfd there are 2! = 2 ways to assign n3 and n4, giving 4 * 2 = 8 possibilities.
3: For 31246 <= n <= 39876, the range of values for d are 31246/99 = 316 to 39876/92 = 433. However, if n1 = 3, then d1 can’t be 3 and must be 4. This gives 412 <= d <= 428 (since d2 can’t be 3 and dfd can’t be 9) making d2 = 1 or 2, and making the minimum value for n = 92 * 412 = 37904. n2 must be 7, 8 or 9. There are only 8 combinations for dfi, dfn, and dfd that don’t have a 3 or 4 and also don’t have both 1 and 2: (2,6,7), (2,8,6), (6,2,8), (6,8,2), (6,8,7), (7,6,2), (7,8,6) and (8,2,6). Six of these have a 2, each of these has a 7 or 8, and two have both a 7 & 8. For d2 = 1, there are 8 ways to assign dfi, dfn, and dfd if n2 = 9, and 6 ways to assign dfi, dfn, and dfd if n2 = 7 or 8, for a total of 2 * 6 + 8 = 20 possibilities for d2 = 1. For d2 = 2, n2 = 9 since both combinations for dfi, dfn, and dfd that don’t have a 2–(6,8,7) and (7,8,6)–have both a 7 & 8. There are 20 + 2 = 22 ways to assign i1, d1, d2, d3, n2, and n5 when n1 = 3 and 2! = 2 ways to assign n3 and n4, giving 22 * 2 = 44 possibilities.
4: For 41236 <= n <= 49876, the range of values for d are 41236/99 = 417 to 49876/92 = 542. However, if n1 = 4, then d1 can’t be 4 and must be 5. This gives 512 <= d <= 538 (since d2 can’t be 4 and dfd can’t be 9) making d2 = 1, 2 or 3 and making the minimum value for n = 92 * 512 = 47104. n2 must be 7, 8 or 9. There are 22 combinations for dfi, dfn, and dfd that don’t have a 4 or 5: (1,2,8), (1,3,7), (1,7,3), (1,8,2), (2,6,7), (2,8,1), (2,8,6), (3,2,6), (3,6,8), (3,7,1), (3,9,7), (6,2,3), (6,2,8), (6,8,2), (6,8,7), (7,3,1), (7,6,2), (7,8,6), (7,9,3), (8,2,1), (8,2,6) and (8,6,3). For d2 = 1, there are {8, 6, 12} = 26 ways to assign dfi, dfn, and dfd for n2 = {7, 8, 9}. For d2 = 2, there are {2, 6, 8} = 16 ways to assign dfi, dfn, and dfd for n2 = {7, 8, 9}. For d2 = 3, there are {8, 2, 12} = 22 ways to assign dfi, dfn, and dfd for n2 = {7, 8, 9}. There are 26 + 16 + 22 = 64 ways to assign i1, d1, d2, d3, n2, and n5 when n1 = 4 and 2! = 2 ways to assign n3 and n4, giving 64 * 2 = 128 possibilities.
5: For 51234 <= n <= 59876, the range of values for d are 51234/99 = 518 to 59876/92 = 650. However, if n1 = 5, then d1 can’t be 5 and must be 6. This gives 612 <= d <= 648 (since dfd can’t be 0 or 9) making d2 = 1, 2, 3 or 4 and making the minimum value for n = 92 * 612 = 56304. n2 can’t be 6 (since d1 = 6), so the minimum value for n is 57123, making the minimum value for d = 57123/92 = 620. So now 621 <= d <= 648 (since dfd can’t be 0) making d2 = 2, 3 or 4 and n2 = 7, 8 or 9. There are 20 combinations for dfi, dfn, and dfd that don’t have a 5 or 6: (1,2,8), (1,3,7), (1,7,3), (1,8,2), (2,4,3), (2,4,8), (2,8,1), (3,4,2), (3,7,1), (3,8,4), (3,9,7), (4,2,7), (4,8,3), (7,2,4), (7,3,1), (7,4,8), (7,9,3), (8,2,1), (8,4,2) and (8,4,7). For d2 = 2, there are {2, 6, 8} = 16 ways to assign dfi, dfn, and dfd for n2 = {7, 8, 9}. For d2 = 3, there are {6, 2, 10} = 18 ways to assign dfi, dfn, and dfd for n2 = {7, 8, 9}. For d2 = 4, there are {4, 6, 8} = 18 ways to assign dfi, dfn, and dfd for n2 = {7, 8, 9}. There are 16 + 18 + 18 = 52 ways to assign i1, d1, d2, d3, n2, and n5 when n1 = 5 and 2! = 2 ways to assign n3 and n4, giving 52 * 2 = 104 possibilities.
6: For 61234 <= n <= 69874, the range of values for d are 61234/99 = 619 to 69874/92 = 759. However, if n1 = 6, then d1 can’t be 6 and must be 7. This gives 712 <= d <= 758 (since dfd can’t be 9) making d2 = 1, 2, 3, 4 or 5 and making the minimum value for n = 92 * 712 = 65504. n2 can’t be 6 or 7, so n2 = 5, 8 or 9 and when n2 = 5, n3 = 8 or 9. There are 12 combinations for dfi, dfn, and dfd that don’t have a 6 or 7: (1,2,8), (1,8,2), (2,4,3), (2,4,8), (2,8,1), (3,4,2), (3,8,4), (4,8,3), (8,2,1) and (8,4,2). For d2 = 1, there are {6, 2, 6} = 14 ways to assign dfi, dfn, and dfd for n2 = {5, 8, 9}. For d2 = 2, there are {2, 0, 2} = 4 ways to assign dfi, dfn, and dfd for n2 = {5, 8, 9}. For d2 = 3, there are {6, 0, 6} = 12 ways to assign dfi, dfn, and dfd for n2 = {5, 8, 9}. For d2 = 4, there are {4, 0, 4} = 8 ways to assign dfi, dfn, and dfd for n2 = {5, 8, 9}. For d2 = 5, there are {2, 12} = 14 ways to assign dfi, dfn, and dfd for n2 = {8, 9}. There are 14 + 4 + 12 + 8 + 14 = 52 ways to assign i1, d1, d2, d3, n2, and n5 when n1 = 6 and 2! = 2 ways to assign n3 and n4, giving 52 * 2 = 104 possibilities. From this we can subtract the {4, 2, 6, 4} = 16 cases for d2 = {1, 2, 3, 4} and n2 = 5 where n3 must be 9 (because 8 is assigned to dfi, dfn, or dfd). This gives 104 – 16 = 88 possibilities.
7: For 71234 <= n <= 79864, the range of values for d are 71234/99 = 720 to 79864/92 = 868. However, if n1 = 7, then d1 can’t be 7 and must be 8. However, if n1 = 7 and d1 = 8, then i1 can’t be 7 or 8, and n/d can’t be 92 or 93. This gives a maximum value for d of 79864/94 = 849, and gives 812 <= d <= 836 (since dfd can’t be 7, 8 or 9) making d2 = 1, 2 or 3 and making the minimum value for n = 94 * 812 = 76328. n2 = 6 or 9. There are 8 combinations for dfi, dfn, and dfd that don’t have a 7 or 8: (1,4,6), (1,6,4), (2,4,3), (3,2,6), (3,4,2), (4,6,1), (6,2,3) and (6,4,1). For d2 = 1, there are {2, 4} = 6 ways to assign dfi, dfn, and dfd for n2 = {6, 9}. For d2 = 2, there are {0, 4} = 4 ways to assign dfi, dfn, and dfd for n2 = {6, 9}. For d2 = 3, there are {0, 3} = 3 ways to assign dfi, dfn, and dfd for n2 = {6, 9}. There are 6 + 4 + 3 = 13 ways to assign i1, d1, d2, d3, n2, and n5 when n1 = 7 and 2! = 2 ways to assign n3 and n4, giving 13 * 2 = 26 possibilities.
8: For 81234 <= n <= 89764, the range of values for d are 81234/99 = 821 to 89764/93 = 965 (if n1 = 8, then i1 can’t be 8, and n/d can’t be 92). However, if n1 = 8, then d1 can’t be 8 and must be 9. Since n2 can’t be 8 or 9, the maximum value for d is the greater of 86543/93 = 930 (where i1 = 7) or 87543/94 = 931 (where i1 = 6). This gives 912 <= d <= 928 (because dfd can’t be 0 or 1) making d2 = 1 or 2 and making the minimum value for n = 93 * 912 = 84816. However, since n3 can’t be 8 or 9, the minimum value for n is actually 85123 and n2 = 5, 6 or 7. There are 15 combinations for dfi, dfn, and dfd that don’t have an 8 or 9: (1,3,7), (1,4,6), (1,6,4), (2,4,3), (2,6,7), (3,2,6), (3,4,2), (3,7,1), (4,2,7), (4,6,1), (6,2,3), (6,4,1), (7,2,4), (7,3,1) and (7,6,2). For d2 = 1, there are {8, 4, 4} = 16 ways to assign dfi, dfn, and dfd for n2 = {5, 6, 7}. For d2 = 2, there are {7, 3, 4} = 14 ways to assign dfi, dfn, and dfd for n2 = {5, 6, 7}. There are 16 + 14 = 30 ways to assign i1, d1, d2, d3, n2, and n5 when n1 = 8 and 2! = 2 ways to assign n3 and n4, giving 30 * 2 = 60 possibilities.
The search space for single-digit i = 8 + 44 + 128 + 104 + 88 + 26 + 60 = 458. This is a reduction of 99.9% for this case.
Two-digit i, cases for i1:
2: For 21 <= i <= 28, then 72 <= n/d <= 79 and the maximum value for d is the greater of 9764/72 = 135 (where i2 = 8) and 9864/73 = 135 (where i2 = 7). This makes d1 = 1 and d2 = 3, giving a range for d of 134 to 134 (since d3 can’t be 5). Since 9876/134 = 73, the minimum value for i is 100 – 73 = 27, making i2 = 7, 8 or 9. There is no way to assign dfi, dfn, and dfd where dfd = 4 and dfi = 7, 8 or 9, and dfn is not 1, 2 or 3. So i1 can’t be 2.
3: For 31 <= i <= 38, then 62 <= n/d <= 69 and the maximum value for d is the greater of 9764/62 = 157 (where i2 = 8) and 9864/63 = 156 (where i2 = 7). This gives a range for d of 124 to 157, and makes d1 = 1 and d2 = 2, 4 or 5. If d1 = 1, then i2 can’t be 1. If i2 is 2, then n/d = 68 and the minimum value for d is 146 (since i is 32 and d3 can’t be 5). Since 146 * 68 > 9876, i2 can’t be 2, making i2 = 4, 6, 7 or 8. The minimum value for n is 124 * 62 = 7688, making n1 = 7, 8 or 9. There are 11 combinations for dfi, dfn, and dfd where dfi = 4, 6, 7 or 8 and that don’t have a 1 or 3: (4,2,7), (6,2,8), (6,8,2), (6,8,7), (7,2,4), (7,4,8), (7,6,2), (7,8,6), (8,2,6), (8,4,2) and (8,4,7). For d2 = 2, the minimum value for n is 124 * 62 = 7688 and there are {0, 0, 4} = 4 ways to assign dfi, dfn, and dfd for n1 = {7, 8, 9}. For d2 = 4, the minimum value for n is 142 * 62 = 8804 and there are {1, 6} = 7 ways to assign dfi, dfn, and dfd for n1 = {8, 9}. For d2 = 5, the minimum value for n is 152 * 62 = 9424 and there are 11 ways to assign dfi, dfn, and dfd when n1 = 9. There are 4 + 7 + 11 = 22 ways to assign i2, d1, d2, d3, n1, and n4 when i1 = 3 and 2! = 2 ways to assign n2 and n3, giving 22 * 2 = 44 possibilities.
4: For 41 <= i <= 48, then 52 <= n/d <= 59 and the maximum value for d is the greater of 9763/52 = 187 (where i2 = 8) and 9863/53 = 186 (where i2 = 7). This gives a range for d of 123 to 187, and makes d1 = 1 and d2 = 2, 3, 5, 6, 7 or 8. There are 14 combinations for dfi, dfn, and dfd that don’t have a 1 or 4: (2,6,7), (2,8,6), (3,2,6), (3,6,8), (3,9,7), (6,2,3), (6,2,8), (6,8,2), (6,8,7), (7,6,2), (7,8,6), (7,9,3), (8,2,6) and (8,6,3). For d2 = 2, the minimum value for n is 123 * 52 = 6396 and there are {2, 2, 2, 4} = 10 ways to assign dfi, dfn, and dfd for n1 = {6, 7, 8, 9}. For d2 = 3, the minimum value for n is 132 * 52 = 6864 and there are {0, 4, 2, 8} = 14 ways to assign dfi, dfn, and dfd for n1 = {6, 7, 8, 9}. For d2 = 5, the minimum value for n is 152 * 52 = 7904 and there are {8, 6, 12} = 26 ways to assign dfi, dfn, and dfd for n1 = {7, 8, 9}. For d2 = 6, the minimum value for n is 162 * 52 = 8424 and there are {2, 0} = 2 ways to assign dfi, dfn, and dfd for n1 = {8, 9}. For d2 = 7, the minimum value for n is 172 * 52 = 8424, but n1 can’t be 8 since i2 is 8 and 172 * 53 = 9116, so n1 = 9 and there are 6 ways to assign dfi, dfn, and dfd. For d2 = 8, the minimum value for n is 182 * 53 = 9696, but since i2 = 7, the largest value for n is 9653; if i2 = 6 then 182 * 54 = 9828, but the largest value for n is 9753, so d2 can’t be 8. There are 10 + 14 + 26 + 2 + 6 = 58 ways to assign i2, d1, d2, d3, n1, and n4 when i1 = 4 and 2! = 2 ways to assign n2 and n3, giving 58 * 2 = 116 possibilities.
5: For 51 <= i <= 58, then 42 <= n/d <= 49 and the maximum value for d is the greater of 9764/42 = 232 (where i2 = 8) and 9864/43 = 229 (where i2 = 7). This gives a range for d of 123 to 218 (because dfd can’t be 0, 1 or 9), and makes (d1, d2) = (1, 2), (1, 3), (1, 4), (1, 6), (1, 7), (1, 8), (1, 9) or (2, 1). None of the combinations for dfi, dfn, and dfd have a 5, so all 36 are possible. For (d1, d2) = (1, 2) the minimum value for n is 123 * 42 = 5166, but n1 can’t be 5, and there are {6, 4, 2, 8} = 20 ways to assign dfi, dfn, and dfd for n1 = {6, 7, 8, 9}. For (d1, d2) = (1, 3) the minimum value for n is 132 * 42 = 5544, but n1 can’t be 5, and there are {7, 6, 4, 14} = 31 ways to assign dfi, dfn, and dfd for n1 = {6, 7, 8, 9}. For (d1, d2) = (1, 4) the minimum value for n is 142 * 42 = 5964, but n1 can’t be 5, and there are {2, 8, 6, 12} = 28 ways to assign dfi, dfn, and dfd for n1 = {6, 7, 8, 9}. For (d1, d2) = (1, 6) the minimum value for n is 162 * 42 = 6804, but n1 can’t be 6, and there are {6, 6, 10} = 32 ways to assign dfi, dfn, and dfd for n1 = {7, 8, 9}. For (d1, d2) = (1, 7) the minimum value for n is 172 * 42 = 7224, but n1 can’t be 7, and there are {4, 14} = 18 ways to assign dfi, dfn, and dfd for n1 = {8, 9}. For (d1, d2) = (1, 8) the minimum value for n is 182 * 43 = 7826, but n1 can’t be 7 because i2 = 7 and 182 * 44 = 8008, so n1 = 9 and there are 8 ways to assign dfi, dfn, and dfd. For (d1, d2) = (1, 9) the minimum value for n is 192 * 43 = 8256, so n1 = 8 and there are 8 ways to assign dfi, dfn, and dfd for n1 = {6, 7, 8, 9}. For (d1, d2) = (2, 1) the minimum value for n is 213 * 42 = 8946, but n1 can’t be 8 because i2 = 8, so n1 = 9 and there are 8 ways to assign dfi, dfn, and dfd. There are 20 + 31 + 28 + 32 + 18 + 8 + 8 + 8 = 153 ways to assign i2, d1, d2, d3, n1, and n4 when i1 = 5 and 2! = 2 ways to assign n2 and n3, giving 153 * 2 = 306 possibilities.
6: For 61 <= i <= 68, then 32 <= n/d <= 39 and the maximum value for d is the greater of 9754/32 = 304 (where i2 = 8) and 9864/33 = 299 (where i2 = 7). This gives a range for d of 123 to 298 (d2 can’t be zero), and makes d1 = 1 or 2. There are 16 combinations for dfi, dfn, and dfd that don’t have a 6 or don’t have both a 1 and 2: (1,3,7), (1,7,3), (2,4,3), (2,4,8), (3,4,2), (3,7,1), (3,8,4), (3,9,7), (4,2,7), (4,8,3), (7,2,4), (7,3,1), (7,4,8), (7,9,3), (8,4,2) and (8,4,7). For d1 = 1 the minimum value for n is 126 * 32 = 4032 (because 123 * 32 = 3936, but n1 can’t be 3 if d3 = 3; 124 * 32 = 3968, but n3 can’t be 6; 124 * 33 = 4092; and d3 can’t be 5), and there are {2, 12, 6, 6, 10} = 36 ways to assign dfi, dfn, and dfd for n1 = {4, 5, 7, 8, 9}. For d1 = 2 the minimum value for n is 213 * 32 = 6816, but n1 can’t be 6, and there are {2, 6, 8} = 16 ways to assign dfi, dfn, and dfd for n1 = {7, 8, 9}. There are 36 + 16 = 52 ways to assign i2, d1, d3, n1, and n4 when i1 = 6 and 3! = 6 ways to assign d2, n2 and n3, giving 52 * 6 = 312 possibilities.
7: For 71 <= i <= 78, then 22 <= n/d <= 29 and the maximum value for d is 9654/22 = 438. This gives a range for d of 123 to 436 (dfd can’t be 7 or 8 when i = 78), and makes d1 = 1, 2, 3 or 4. There are 22 combinations for dfi, dfn, and dfd that don’t have a 7: (1,2,8), (1,4,6), (1,6,4), (1,8,2), (2,4,3), (2,4,8), (2,8,1), (2,8,6), (3,2,6), (3,4,2), (3,6,8), (3,8,4), (4,6,1), (4,8,3), (6,2,3), (6,2,8), (6,4,1), (6,8,2), (8,2,1), (8,2,6), (8,4,2) and (8,6,3). For d1 = 1 the minimum value for n1 = 3 (because 134 * 22 = 2948, but n3 can’t be 4 if d3 = 4; 136 * 22 = 2992, but n2 and n3 can’t both be 9), and there are {6, 8, 14, 6, 4, 2, 14} = 54 ways to assign dfi, dfn, and dfd for n1 = {3, 4, 5, 6, 8, 9}. For d1 = 2 the minimum value for n is 213 * 22 = 4686, and there are {1, 8, 2, 4, 8} = 23 ways to assign dfi, dfn, and dfd for n1 = {4, 5, 6, 8, 9}. For d1 = 3 the minimum value for n is 312 * 22 = 6864, and there are {6, 4, 14} = 24 ways to assign dfi, dfn, and dfd for n1 = {6, 8, 9}. For d1 = 4 the minimum value for n is 412 * 22 = 9064, and there are 12 ways to assign dfi, dfn, and dfd for n1 = 9. There are 54 + 23 + 24 + 12 = 113 ways to assign i2, d1, d3, n1, and n4 when i1 = 7 and 3! = 6 ways to assign d2, n2 and n3, giving 113 * 6 = 678 possibilities.
8: For 81 <= i <= 87, then 13 <= n/d <= 19 and the maximum value for d is 9654/13 = 742. This gives a range for d of 123 to 742, and makes d1 = 1, 2, 3, 4, 5, 6 or 7. There are 18 combinations for dfi, dfn, and dfd that don’t have an 8: (1,3,7), (1,4,6), (1,6,4), (1,7,3), (2,4,3), (2,6,7), (3,2,6), (3,4,2), (3,7,1), (3,9,7), (4,2,7), (4,6,1), (6,2,3), (6,4,1), (7,2,4), (7,3,1), (7,6,2) and (7,9,3). For d1 = 1 the minimum value for n1 is 2 (because 1976/13 = 152, so if d1 = 1, then n1 <= 1), and there are {2, 4, 6, 10, 6, 4, 8} = 40 ways to assign dfi, dfn, and dfd for n1 = {2, 3, 4, 5, 6, 7, 9}. For d1 = 2 the minimum value for n1 is 3 (because 213 * 13 = 2769, but n1 can’t be 2 if d1 = 2), and there are {4, 6, 10, 6, 4, 8} = 38 ways to assign dfi, dfn, and dfd for n1 = {3, 4, 5, 6, 7, 9}. For d1 = 3 the minimum value for n is 312 * 13 = 4056, and there are {2, 8, 3, 4, 8} = 35 ways to assign dfi, dfn, and dfd for n1 = {4, 5, 6, 7, 9}. For d1 = 4 the minimum value for n is 412 * 13 = 5356, and there are {10, 6, 2, 9} = 27 ways to assign dfi, dfn, and dfd for n1 = {5, 6, 7, 9}. There are 40 + 38 + 35 + 27 = 140 ways to assign i2, d1, d3, n1, and n4 when i1 = 8 and 3! = 6 ways to assign d2, n2 and n3, giving 140 * 6 = 840 possibilities.
9: For 91 <= i <= 98, then 2 <= n/d <= 9. For this range it makes more sense to look at each value for i2 = {1, 2, 3, 4, 6, 7, 8} separately.
i2 = 1, n/d = 9: In this case d1 > n1 and the combinations of dfi, dfn and dfd where dfi = 1 that don’t have a 9 are (1,2,8), (1,3,7), (1,4,6), (1,6,4), (1,7,3) and (1,8,2). If n1 = 2, the maximum value for d = 2876/9 = 319, but d2 can’t be 0 or 1, so n1 can’t be 2. If n1 = 3, the maximum value for d = 3876/9 = 430, which gives a range for d of 426 to 428 (because dfd can’t be 0, 1, 4, 5 or 9), but there are no combinations for dfn and dfd that don’t have a 2, 3 or 4, so n1 can’t be 3. If n1 = 4, the maximum value for d = 4876/9 = 541, which gives a range for d of 523 <= d <= 538 (because dfd can’t be 0, 1 or 9), and there are {2, 2} = 4 ways to assign dfn and dfd for d2 = {2, 3}. If n1 = 5, the maximum value for d = 5876/9 = 652, which gives a range for d of 623 <= d <= 648 (because d2 can’t be 5 and dfd can’t be 9), and there are {2, 2, 4} = 8 ways to assign dfn and dfd for d2 = {2, 3, 4}. If n1 = 6, the maximum value for d = 6874/9 = 763, which gives a range for d of 723 <= d <= 758 (because d2 can’t be 6 and dfd can’t be 9), and there are {0, 2, 2, 2} = 6 ways to assign dfn and dfd for d2 = {2, 3, 4, 5}. If n1 = 7, the maximum value for d = 7864/9 = 873, which gives a range for d of 823 <= d <= 867 (because d2 can’t be 7 and dfd can’t be 9), and there are {2, 2, 0, 2, 0} = 6 ways to assign dfn and dfd for d2 = {2, 3, 4, 5, 6}. n1 can’t be 8 because d1 can’t be 9. There are 4 + 8 + 6 + 6 = 24 ways to assign d1, d2, d3, n1, and n4 when i = 91 and 2! = 2 ways to assign n2 and n3, giving 24 * 2 = 48 possibilities.
i2 = 2, n/d = 8: The combinations of dfi, dfn and dfd where dfi = 2 that don’t have a 9 are (2,4,3), (2,4,8), (2,6,7), (2,8,1) and (2,8,6). If n1 = 1, the maximum value for d = 1876/8 = 234, but d1 can’t be 2, so n1 can’t be 1. If n1 = 3, the maximum value for d = 3876/8 = 484, but n2 and d2 can’t both be 8 and 480 * 8 = 3840, d2 can’t be 8 when n1 = 3, which gives a range for d of 416 <= d <= 478, and there are {2, 3, 1, 2} = 8 ways to assign dfn and dfd for d2 = {1, 5, 6, 7}. If n1 = 4, the minimum value for d = 4136/8 = 518 and the maximum value for d = 4876/8 = 609, which gives a range for d of 518 <= d <= 587 (because d2 can’t be 0 or 9 and dfd can’t be 9), and there are {0, 3, 1, 2, 1} = 7 ways to assign dfn and dfd for d2 = {1, 3, 6, 7, 8}. If n1 = 5, the minimum value for d = 5134/8 = 642 and the maximum value for d = 5876/8 = 734, but n3 and d1 can’t both be 7, so the maximum value for d = 5764/8 = 733, which gives a range for d of 643 <= d <= 731, and there are {0, 3, 1, 3, 1} = 8 ways to assign dfn and dfd for (d1, d2) = {(6,4), (6,7), (6,8), (7,1), (7,3)}. If n1 = 6, the minimum value for d = 6134/8 = 767 and the maximum value for d = 6874/8 = 859, but n2 and d1 can’t both be 8, so the maximum value for d = 6754/8 = 844, which gives a range for d of 781 <= d <= 843, and there are {1, 1, 0, 0} = 2 ways to assign dfn and dfd for (d1, d2) = {(7,8), (8,1), (8,3), (8,4)}. If n1 = 7, the minimum value for d = 7134/8 = 892, which is larger than 864, the largest possible value for d, so n1 < 7. There are 8 + 7 + 8 + 2 = 25 ways to assign d1, d2, d3, n1, and n4 when i = 92 and 2! = 2 ways to assign n2 and n3, giving 25 * 2 = 50 possibilities.
i2 = 3, n/d = 7: The combinations of dfi, dfn and dfd where dfi = 3 that don’t have a 9 are (3,2,6), (3,4,2), (3,6,8), (3,7,1) and (3,8,4). If n1 = 1, the maximum value for d = 1876/7 = 268, which gives a range for d of 246 to 268, and there are {1, 2, 1} = 4 ways to assign dfn and dfd for d2 = {4, 5, 6}. If n1 = 2, the minimum value for d = 2146/7 = 307 and the maximum value for d = 2876/7 = 410, and d1 can’t be 3, so n1 can’t be 2. If n1 = 4, the minimum value for d = 4126/7 = 590 and the maximum value for d = 4876/7 = 696, which gives a range for d of 612 <= d <= 687 (because d2 can’t be 0 or 9 and dfd can’t be 9), and there are {0, 1, 1, 0, 1} = 3 ways to assign dfn and dfd for d2 = {1, 2, 5, 6, 7, 8}. If n1 = 5, the minimum value for d = 5124/7 = 732 and the maximum value for d = 5876/7 = 839, which gives a range for d of 741 <= d <= 827 (because d2 can’t be 3 and dfd can’t be 9), and there are {2, 2, 2, 2, 1} = 9 ways to assign dfn and dfd for (d1, d2) = {(7,4), (7,6), (7,8), (8,1), (8,2)}. If n1 = 6, the minimum value for d = 6124/7 = 875, which is greater than the largest available value for d of 874, so n1 < 6. There are 4 + 3 + 9 = 16 ways to assign d1, d2, d3, n1, and n4 when i = 93 and 2! = 2 ways to assign n2 and n3, giving 16 * 2 = 32 possibilities.
i2 = 4, n/d = 6: The combinations of dfi, dfn and dfd where dfi = 4 that don’t have a 9 are (4,2,7), (4,6,1) and (4,8,3). If n1 = 1, dfd = 3 or 7 and the maximum value for d = 1876/6 = 312, which gives a range for d of 237 to 287, and there are {0, 1, 1, 1, 0} = 3 ways to assign dfn and dfd for d2 = {3, 5, 6, 7, 8}. If n1 = 2, the minimum value for d = 2136/6 = 356 and the maximum value for d = 2876/6 = 479, and d1 can’t be 3 or 4, so n1 can’t be 2. If n1 = 3, the minimum value for d = 3126/6 = 521 and the maximum value for d = 3876/6 = 646, which gives a range for d of 521 <= d <= 628 (because d2 can’t be 3 or 4 and dfd can’t be 9), and there are {1, 1, 1, 2, 1, 0} = 6 ways to assign dfn and dfd for (d1, d2) = {(5,2), (5,6), (5,7), (5,8), (6,1), (6,2)}. If n1 = 5, the minimum value for d = 5123/6 = 854 and the maximum value for d = 5876/6 = 979, which gives a range for d of 861 <= d <= 876 (because d2 can’t be 5 or 9, and dfd can’t be 9), and there are {1, 1} = 2 ways to assign dfn and dfd for d2 = {6, 7}. n1 < n/d, so n1 < 6. There are 3 + 6 + 2 = 11 ways to assign d1, d2, d3, n1, and n4 when i = 94 and 2! = 2 ways to assign n2 and n3, giving 11 * 2 = 22 possibilities.
i2 = 6, n/d = 4: The combinations of dfi, dfn and dfd where dfi = 6 that don’t have a 9 are (6,2,3), (6,2,8), (6,4,1), (6,8,2) and (6,8,7). If n1 = 1, the minimum value for d = 1234/4 = 309 and the maximum value for d = 1876/4 = 469, which gives a range for d of 324 to 458 (because d2 can’t be 1 or 6 and dfd can’t be 9), and there are {1, 3, 3, 2, 0, 1, 3, 4} = 17 ways to assign dfn and dfd for (d1, d2) = {(3,2), (3,4), (3,5), (3,7), (3,8), (4,2), (4,3), (4,5)}. If n1 = 2, the minimum value for d = 2134/4 = 534 and the maximum value for d = 2874/4 = 718, which gives a range for d of 534 to 718, and there are {2, 1, 1, 1, 0} = 5 ways to assign dfn and dfd for (d1, d2) = {(5,3), (5,4), (5,7), (5,8), (7,1)}. If n1 = 3, the minimum value for d = 3124/4 = 781 and the maximum value for d = 3874/4 = 968, which gives a range for d of 781 <= d <= 874 (because no digits in d can be 9), and there are {1, 0, 1, 0, 1, 1} = 4 ways to assign dfn and dfd for (d1, d2) = {(7,8), (8,1), (8,2), (8,4), (8,5), (8,7)}. n1 < n/d, so n1 < 4. There are 17 + 5 + 4 = 26 ways to assign d1, d2, d3, n1, and n4 when i = 96 and 2! = 2 ways to assign n2 and n3, giving 26 * 2 = 52 possibilities.
i2 = 7, n/d = 3: The combinations of dfi, dfn and dfd where dfi = 7 that don’t have a 9 are (7,2,4), (7,3,1), (7,4,8), (7,6,2) and (7,8,6). If n1 = 1, the minimum value for d = 1234/3 = 412 and the maximum value for d = 1864/3 = 621, which gives a range for d of 423 to 586 (because no digits in d can be 0, 1 or 9, and dfd can’t be 9), and there are {1, 2, 0, 1, 2, 4, 2, 2, 2} = 16 ways to assign dfn and dfd for (d1, d2) = {(4,2), (4,5), (4,6), (4,8), (5,2), (5,3), (5,4), (5,6), (5,8)}. If n1 = 2, the minimum value for d = 2134/3 = 712 and the maximum value for d = 2864/3 = 954, which gives a range for d of 813 to 864 (because no digits in d can be 7 or 9), and there are {0, 0, 1, 1, 1} = 3 ways to assign dfn and dfd for d2 = {1, 3, 4, 5, 6}. n1 < n/d, so n1 < 3. There are 16 + 3 = 19 ways to assign d1, d2, d3, n1, and n4 when i = 97 and 2! = 2 ways to assign n2 and n3, giving 19 * 2 = 38 possibilities.
i2 = 8, n/d = 2: Since n/d = 2, n1 = 1. The combinations of dfi, dfn and dfd where dfi = 8 that don’t have a 1 or 9 are (8,2,6), (8,4,2), (8,4,7) and (8,6,3). The minimum value for d = 1234/2 = 617 and the maximum value for d = 1764/2 = 882, which gives a range for d of 623 to 764 (because no digits in d can be 0, 1, 8 or 9, and dfd can’t be 9), and there are {1, 2, 0, 2, 1, 1, 2, 2, 3, 1} = 15 ways to assign dfn and dfd for (d1, d2) = {(6,2), (6,3), (6,4), (6,5), (6,7), (7,2), (7,3), (7,4), (7,5), (7,6)}. There are 15 ways to assign d1, d2, d3, n1, and n4 when i = 98 and 2! = 2 ways to assign n2 and n3, giving 15 * 2 = 30 possibilities.For 91 <= i <= 98, there are 48 + 50 + 32 + 22 + 52 + 38 + 30 = 272 possibilities.
The search space for two-digit i = 44 + 116 + 306 + 312 + 768 + 840 + 272 = 2658. This is a reduction of 99.3% for this case.
Final tally
The final total search space is 458 + 2658 = 3116 possible permutations of the digits 1 to 9 that produce a mixed fraction that equals 100.
By pruning, the search space is reduced by over 99.57%. Of the 7 single-digit and 14 two-digit sub-spaces, 5 contained a result (single-digit i = 3, two-digit 81 <= i <= 87, i = 91, i = 94, and i = 96). Those sub-spaces contained 44 + 840 + 48 + 22 + 52 = 996 possibilities containing 1 + 3 + 3 + 1 + 3 = 11 results.
- 6697 views
- 1 answers
- 1 votes
-
- 6391 views
- 2 answers
- 1 votes
-
As the first answer from neha points out, it is not a triangle and you can determine that by looking at the ratios of the red and green right triangles. The green triangle has legs of 2 and 5 (2/5 = 0.4 ratio) and the red triangle has legs of 3 and 8 (3/8 = .375 ratio).
The full right triangle has legs of 5 and 13 (5/13 = .3846…) which is between the ratios of the other two triangles. This triangle should have an area of 5 * 13 / 2 = 32.5 squares. Adding up the areas of the pieces we have:
Yellow: 7
Light green: 8
Green triangle: 2 * 5 / 2 = 5
Red triangle: 3 * 8 / 2 = 12Total = 7 + 8 + 5 + 12 = 32
There is 0.5 squares missing in the top figure due to the hypotenuse being bowed in and 0.5 squares extra in the bottom figure due to the hypotenuse being bowed out. The seemingly missing square in the bottom figure is accounted for by the 0.5 + 0.5 = 1 square.
- 6679 views
- 2 answers
- 1 votes
-
This depends on the definition of “a bounce”.
In order for anything to bounce, it must first absorb energy and then release the energy. Basically, the energy is temporarily stored in the distortion of the object, and then released when the object “springs” back to its original shape. The deformation of the ball causes the ball to compress. The ball can be considered to have stopped bouncing when the energy released by springing back is less than the amount of energy required to lift the ball by a distance equal to its compression. When the energy released reaches that point, the ball is at rest.
Unfortunately, nothing in the question allows us to determine how much the ball deforms when it bounces, thus the number of bounces can’t be determined. The answer is most certainly not “infinite“, which is the naive answer you get from considering the geometric sequence of a “perfect” ball that doesn’t compress at all when it bounces.
- 4031 views
- 3 answers
- 0 votes
-
Mr. Blue : red shirt
Mr. Red : white shirt
Mr. White : blue shirtMr. Blue is not wearing the blue shirt, nor is he wearing the white shirt. Therefore Mr. Blue is wearing the red shirt. Since Mr. White can’t wear the white shirt, he must be wearing the blue shirt, leaving the white shirt for Mr. Red.
- 4725 views
- 3 answers
- 1 votes
-
Nobody ever says they belong to the lie tribe–both liars and truthtellers will claim to belong to the truth tribe. Therefore, the second person is lying. Since that matches what the third person said, the third person belongs to the truth tribe.
- 10657 views
- 2 answers
- 1 votes
-
Assuming neither the array nor sub-array can be empty, there are two possibilities.
- Either all values in the array are negative, in which case the sub-array with the largest sum is the 1-element sub-array containing the maximum value, or
- There are non-negative values in the array and the sub-array is bounded by negative value(s) and/or the maximum/minimum indexes.
The algorithm is to iterate through the array calculating the sum. Whenever the sum drops below zero, reset the sum to zero and reset the low index. Whenever the sum exceeds the maximum sum, record the new maximum and the sub-array indexes for the maximum.
Given an array a of size s:
msum = smallest negative integer mlow = -1 mhigh = -1 low = -1 sum = 0 for i = 0; i < s; i = i + 1 { if a[i] < 0 { if a[i] > msum { msum = a[i] mlow = mhigh = i } else { sum += a[i] if sum < 0 { sum = 0 low = -1 } } } else { if low == -1 { low = i } sum += a[i] if sum > msum { mlow = low msum = sum mhigh = i } } } // sub-array is a[mlow..mhigh] with a sum of msum- 3790 views
- 1 answers
- 0 votes