It might be that if you are in a particularly mathematical frame of mind you are trying to use a three dimensional co-ordinate system and a matrix transform to project the 45° angles in the corners in to a different plane. By all means. But it’s not necessary, essentially this is a 2D problem, it’s just about finding the right two dimensions to work in. Let’s add another line to the diagram and see how we go.

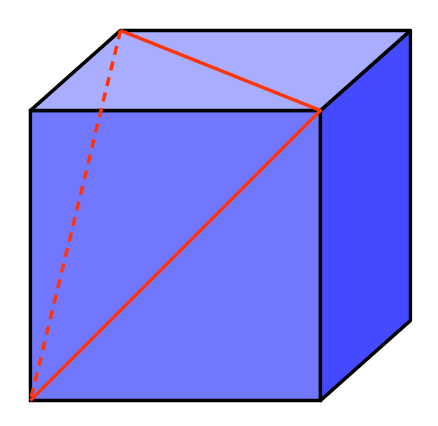
Any clearer? The dotted line completes a triangle. What’s more since all it’s edges are made up of diagonals from the squares, they are all the same length, it is an equilateral triangle. Like all equilateral triangles it’s internal angles are each 60°

A problem I have found with these 3D nets is not everyone sees them the same, it’s like an optical illusion. So at some point over the next few images it should become clear what I’m driving at…




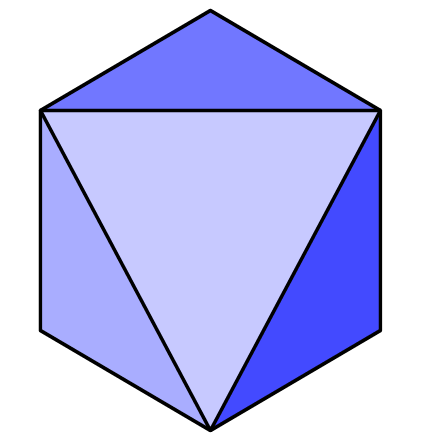
And finally, just because we can.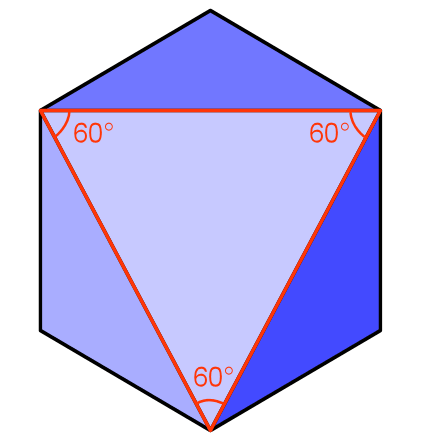

Vector Maths

As I’ve said before it’s my intention that anyone using this site does not need formal maths training. But where there is an obvious maths solution I will try to include it.

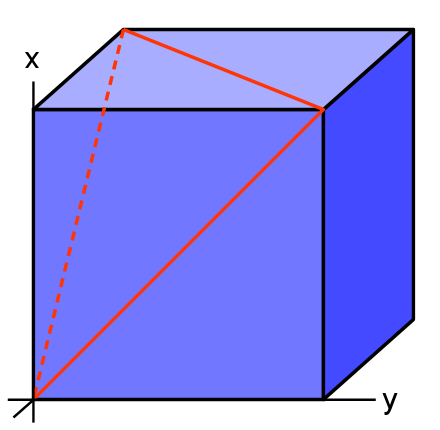
The above diagram shows a standard right handed co-ordinate system with the label on the z axis hidden. We will calculate the angle of the two red lines that meet at the origin. The first being defined as (1,1,0) and the second (1,0,1)

The angle between to vectors is given by:
cos θ = (u•v) / (|u||v|)
cos θ = (1•1 + 1•0 + 0•1) / (√2√2)
cos θ = 1/2
⇒ θ = π/3 or 60°

In order that there is no collision we require that all the ants move in the same direction. Either all clockwise or all anticlockwise.

We assume the ants have a 50/50 chance of picking either direction. So the probability of them all deciding to go clockwise is given by ½•½•½ = 0.125

The probability of them all deciding to go anticlockwise equally is given by ½•½•½ = 0.125

Either of these will do so we can add the probabilities to make 0.25

There is another approach that perhaps requires slightly less understanding of probability. With three things each having two choices we have 2x2x2 = 8 possible configurations. If ‘A’ indicates anticlockwise and ‘C’ clockwise they are AAA, AAC, ACA, ACC, CAA, CAC, CCA & CCC. Of these 8 only 2 are of use to us. AAA and CCC. 2 of 8 is ¼ or 0.25

Square, N sided Polygon

Using the first approach for the triangle we had 2•½•½•½ or 2•(½^n) or 1/2^n-1 or 2^-(n-1) where n was equal to 3. We can see trivially that for a square the answer will be 1/8

Using the other approach we have that there are 2ⁿ configurations, of which 2 will be useful to us. 2/2ⁿ brings us to 1/2^n-1

Assumptions

I think it’s fairly clear that there are no real ants, the ants are just a device for explaining the puzzle. Nonetheless assumptions might be that the ants direction picking is unbiased, and that they move with the same speed.