Brain Teasers & Puzzles
-
A park contains paths that intersect at various places. The intersections all have the properties that they are 3-way intersections and that, with one exception, they are indistinguishable from each other. The one exception is an intersection where there is a restaurant. The restaurant is reachable from everywhere in the park. Your task is to find your way to the restaurant.
The park has strict littering regulations, so you are not allowed to modify the paths or intersections (for example, you are not allowed to leave a note an intersection saying you have been there). However, you are allowed to do some bookkeeping on a pad of paper that you bring with you at all times (in the computer-science parlance, you are allowed some state). How can you find the restaurant?
You may assume that once you enter an intersection, you can continue to the left, continue to the right, or return to where you just came from.
Submit Solution- 1,443.0K views
- 0 answers
- 0 votes
-
Given is a (possibly enormous) rectangular chocolate bar, divided into small squares in the usual way. The chocolate holds a high quality standard, except for the square in the lower left-hand corner, which is poisonous. Two players take turns eating from the chocolate in the following manner: The player whose turn it is points to any one of the remaining squares, and then eats the selected square and all squares positioned above the selected square, to the right of the selected square, or both above and to the right of the selected square. Note, although the board starts off rectangular, it may take on non-rectangular shapes during game play. The object of the game is to avoid the poisonous square. Assuming the initial chocolate bar is larger than 1×1, prove that the player who starts has a winning strategy.
Hint: To my knowledge, no efficient strategy for winning the game is known. That is, to decide on the best next move, a player may need to consider all possible continuations of the game. Thus, you probably want to find a non-constructive proof. That is, to prove that the player who starts has a winning strategy, prove just the existence of such a strategy; in particular, steer away from proofs that would construct a winning strategy for the initial player.
Submit Solution- 1,443.4K views
- 0 answers
- 0 votes
-
You are given an irreflexive symmetric (but not necessarily transitive) “enemies” relation on a set of people. In other words, if person A is an enemy of a person B, then B is also an enemy of A. How can you divide up the people into two houses in such a way that every person has at least as many enemies in the other house as in their own house?
Hint: Planar configuration of straight connecting lines puzzle may provide a hint to solving this puzzle.
Submit Solution- 1,443.2K views
- 0 answers
- 0 votes
-
Given an even number of points in general positions on the plane (that is, no three points co-linear), can you partition the points into pairs and connect the two points of each pair with a single straight line such that the straight lines do not overlap?
Submit Solution- 1,443.2K views
- 0 answers
- 0 votes
-
Someone picks, at their will, two cards from a deck of cards. The cards have different numbers, so one is higher than the other. (In other words, the person picks two distinct numbers in the inclusive range 1 through 13.) The cards are placed face down on a table in front of you. You get to choose one of the cards and turn it face up. Now, you will select one of the two cards (one of whose face you can see, the other one you can’t). If you select the highest card, you win. Design a card-selection strategy for which your chance of winning is strictly greater than 50%.
Submit Solution- 1,442.9K views
- 0 answers
- 0 votes
-
Fill in the clues to reveal the hidden message, in this holiday and cold weather puzzle, from us to you.
Using the clues given, fill in the grid boxes with the answers. In the grid, each horizontal row is one clue and the clues should be entered from the top down. So the first horizontal row goes with clue 1, the second horizontal row goes with clue 2, etc. When the grid is complete, read the highlighted boxes from top to bottom for the hidden message.
HINT: Some of the clues are one word, some are two. Don’t leave spaces between the words when entering a two word answer.
- The Coldest Season of the Year
- Spicy, hot drink to ward off chills
- For kissing your beau under
- A hot stone for your feet & a horse to pull you through the snow
- Zipping down the mountain trails, diamond back to bunny hill
- Warmers for your hands
- Tasty drink that’s good with brandy & nutmeg added
- These sparkling beauties are nature made
- Green trailing plant
- The cookie that makes a house
- Festive greens for your front door
- Red & white sticks of pure pleasure
- No two alike they mantle the ground in cold weather
- Pretty plants with red leaves that form the flower
- Something for the fireplace
- Father Time and Baby _____ ________
- Long tailed headgear with a pompom on the end
- Waltzing around the icy pond
- Gaily wrapped with a bright red bow
- This cake like dessert can be made using the real fruit
- This plant has sharp green leaves and little red berries
- String these on the trees – inside and out
- Three balls of snow, a felt hat and a carrot nose
- The horses prance while wearing these
- An Eskimo’s house
- Down the hill on the snow – whee!
- Sing a merry song to your neighbors
- If you go to one you should bring a gift for the hostess
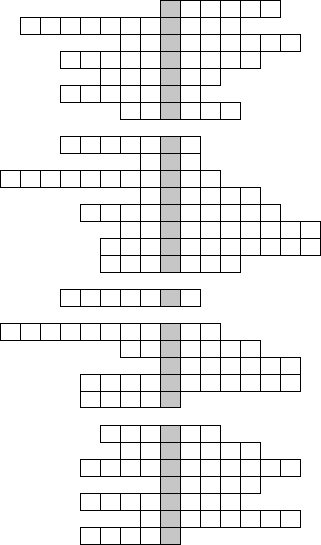 Submit Solution
Submit Solution- 1,443.5K views
- 0 answers
- 0 votes
-
Each of the following phrases below describes the name of a popular game. The dashes on the left side of each phrase represent the name of the game the phrase describes (Note: one dash is one letter, a space signifies a new word). Can you decipher the name of each of the games below?
(Hint: Not all of the clues pertain to the game itself. Some of the clues refer to the actual meaning of the word or phrase by which the game is named. Also, some of the games are board games, some card games, and some are games designed for a group of people.)1. _ _ _ _ _ an African game using beans (1 word) 2. _ _ _ _ _ capture the king to win the game (1 word) 3. _ _ _ _ _ _ _ _ jump over the men to crown a king (1 word) 4. _ _ _ _ _ _ _ turning over the two-colored piece is the name of the game (1 word) 5. _ _ _ _ _ _ _ _ _ _ _ it crashed in 1929 (2 words) 6. _ _ _ _ _ with deepest apologies (1 word) 7. _ _ _ _ _’_ _ _ _ a successful overthrow or takeover (2 words) 8. _ _ _ _ _ _ _ _ a dictionary helps with this game (1 word) 9. _ _ _ _ _ _ _ _ _ _ a French card game where mileage counts (2 words) 10. _ _ _ _ you only have one (1 word) Submit Solution- 1,443.0K views
- 0 answers
- 0 votes
-
Each of the following phrases below describes the name of a popular game. The dashes on the left side of each phrase represent the name of the game the phrase describes (Note: one dash is one letter, a space signifies a new word). Can you decipher the name of each of the games below?
(Hint: Not all of the clues pertain to the game itself. Some of the clues refer to the actual meaning of the word or phrase by which the game is named. Also, some of the games are board games, some card games, and some are games designed for a group of people.)1. _ _ _ _ _ _ _ _ _ _ a dictionary of pictures (1 word) 2. _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ Sherlock Holmes’ address (3 words) 3. _ _ _ _ _ _ _ _ _ _ _ _ the police department of London (2 words) 4. _ _ _ _ _ _ to puzzle or confuse the mind (1 word) 5. _ _ _ _ _ _ _ _ _ _ _ _ _ to succeed, fail, or tie (3 words) 6. _ _ _ _ _ _ _ _ a game of skill to win the flag (1 word) 7. _ _ _ _ _ _ _ _ _ _ _ flip your chips to win the game (1 word) 8. _ _ _ _ _ _ _ _ _ _ double or nothing (3 words) 9. _ _ _ _ _ five card stud is one type (1 word) 10. _ _ _ _ _ _ _ a type of storm (1 word) Submit Solution- 1,442.8K views
- 0 answers
- 0 votes
-
Each of the following phrases below describes the name of a popular game. The dashes on the left side of each phrase represent the name of the game the phrase describes (Note: one dash is one letter, a space signifies a new word). Can you decipher the name of each of the games below?
(Hint: Not all of the clues pertain to the game itself. Some of the clues refer to the actual meaning of the word or phrase by which the game is named. Also, some of the games are board games, some card games, and some are games designed for a group of people.)1. _ _ _ _ _ _ _ _ _ _ _ _ _ _ the luck of life or just plain fate (3 words) 2. _ _ _ _ _ _ _ _ _ _ _ _ _ _ the pursuit is purely trivial (2 words) 3. _ _ _ _ _ _ ‘_’ _ _ _ _ _ _ _ going up or down? (3 words) 4. _ _ _ _ _ _ _ _ do not pass go (1 word) 5. _ _ _ _ some are calculated (1 word) 6. _ _ _ _ Sherlock Holmes always finds them (1 word) 7. _ _ _ _ _ _ _ _ _ uses the theme of Hansel and Gretal (1 word) 8. _ _ _ _ _ _ _ _ dodge the board traps and laser fire to reach the flags first (2 words) 9. _ _ _ _ _ _ _ _ exclamation or shout (1 word) 10. _ _ _ _ _ _ _ _ honest people have them, liars don’t (1 word) Submit Solution- 1,444.2K views
- 0 answers
- 0 votes
-
Round 1- PuzzleFry
Each of the clues below refers to a five-letter word that contains either ‘HI’ or ‘LO’ within it. Can you find all of them?
- dental care
- the sound a bird makes
- something a flower does
- \”Stop and _________.\”
- the navy has them
- how water comes from a faucet
- comes from a hen
- what you see if you hurt yourself
- something woven
- helps keep track of time
Submit Solution- 1,444.8K views
- 0 answers
- 0 votes
More puzzles to try-

How did the officer know?
A police officer was walking outside of a diner. He heard somebody yell inside the diner “No, John not the ...Read More »
Hourglasses puzzle
You have two hourglasses. One measured 7 minutes and the other 11 minutes. How will you measure the 15 minutes ...Read More »
Ghost in House riddle
What room in your house do ghosts avoid?Read More »
Work with different statement riddle
Three working females have different type of work. If only one of statements 1, 2 and 3 are true, can ...Read More »
Name The Country
It begins where the time ends. Its second is an expression of surprise. Its third is a question. Its fourth ...Read More »
Can you find out the missing number?
Can you find out the missing number? ? 4 5 3 5 9 5 7 10 3Read More »
Count the Triangle
Can you count the number of triangles in the picture below?Read More »
I can Sweet or Bitter
I am sometimes honest, Sometimes dishonest I can be sweet and also bitter I can hurt you real bad and ...Read More »
digit puzzle
What 5 digit number am I thinking of. It has two prime digits. Digit 3 is the highest digit. Digit ...Read More »
Wealth Transfer
A wealthy old man wished to leave his fortune to one of his three children before his death. The old ...Read More »
Fill the Required Number Puzzle
Replace the question mark in the picture below.Read More »
No life but die
I have no life, but I can die. What am I?Read More »
Doctor without Doctor
There was a minor accident with a doctor’s son but the doctor noticed no major injury. After the treatment, the ...Read More »
Takes years to rebuild
It takes months to build, seconds to destroy, and years to rebuild. What is it?Read More »
Relationship Riddle
A conversation between 2 people: A – “Hello. Is this XYZ?” B – “Yes. May I know who is this?” ...Read More »
Lines of Balls
You have 10 balls with you. A friend of yours out of nowhere asks you to place those ten balls ...Read More »
Twice ten are six of us riddle
Twice ten are six of us, Six are but three of us, Nine are but four of us; What can ...Read More »
Pocket Money riddle
Last weekend I was given my pocket money, which is meant to last me all week. On Monday, I spent ...Read More »
I carry my master and my master carries me riddle
I carry my master and my master carries me What is it?Read More »
How many vegetables can grow off of the vine?
A tomato vine is 3 meters long. The bottom foot of the vine doesn’t grow any tomatoes but the rest ...Read More »


