Hard Puzzles
-
- 1,642.0K views
- 3 answers
- 0 votes
-
Also known as Hempel’s Paradox, for the German logician who proposed it in the mid-1940s, the Raven Paradox begins with the apparently straightforward and entirely true statement that “all ravens are black.”
The paradox here is that Hempel has apparently proved that seeing an apple provides us with evidence, no matter how unrelated it may seem, that ravens are black. It’s the equivalent of saying that you live in New York is evidence that you don’t live in L.A., or that saying you are 30 years old is evidence that you are not 29. Just how much information can one statement actually imply anyway?
View SolutionSubmit Solution- 1,641.1K views
- 1 answers
- 0 votes
-
Imagine that a farmer has a sack containing 100 lbs of potatoes. The potatoes, he discovers, are comprised of 99% water and 1% solids, so he leaves them in the heat of the sun for a day to let the amount of water in them reduce to 98%. But when he returns to them the day after, he finds his 100 lb sack now weighs just 50 lbs. How can this be true? Well, if 99% of 100 lbs of potatoes is water then the water must weigh 99 lbs. The 1% of solids must ultimately weigh just 1 lb, giving a ratio of solids to liquids of 1:99. But if the potatoes are allowed to dehydrate to 98% water, the solids must now account for 2% of the weight—a ratio of 2:98, or 1:49—even though the solids must still only weigh 1lb. The water, ultimately, must now weigh 49lb, giving a total weight of 50lbs despite just a 1% reduction in water content. Or must it?
Although not a true paradox in the strictest sense, the counterintuitive Potato Paradox is a famous example of what is known as a veridical paradox, in which a basic theory is taken to a logical but apparently absurd conclusion.
View SolutionSubmit Solution- 1,642.9K views
- 1 answers
- 0 votes
-
In his final written work, Discourses and Mathematical Demonstrations Relating to Two New Sciences (1638), the legendary Italian polymath Galileo Galilei proposed a mathematical paradox based on the relationships between different sets of numbers. On the one hand, he proposed, there are square numbers—like 1, 4, 9, 16, 25, 36, and so on. On the other, there are those numbers that are not squares—like 2, 3, 5, 6, 7, 8, 10, and so on. Put these two groups together, and surely there have to be more numbers in general than there are justsquare numbers—or, to put it another way, the total number of square numbers must be less than the total number of square and non-square numbers together. However, because every positive number has to have a corresponding square and every square number has to have a positive number as its square root, there cannot possibly be more of one than the other.
Confused? You’re not the only one. In his discussion of his paradox, Galileo was left with no alternative than to conclude that numerical concepts like more, less, or fewer can only be applied to finite sets of numbers, and as there are an infinite number of square and non-square numbers, these concepts simply cannot be used in this context.
View SolutionSubmit Solution- 1,641.4K views
- 1 answers
- 1 votes
-
Imagine a fletcher (i.e. an arrow-maker) has fired one of his arrows into the air. For the arrow to be considered to be moving, it has to be continually repositioning itself from the place where it is now to any place where it currently isn’t. The Fletcher’s Paradox, however, states that throughout its trajectory the arrow is actually not moving at all. At any given instant of no real duration (in other words, a snapshot in time) during its flight, the arrow cannot move to somewhere it isn’t because there isn’t time for it to do so. And it can’t move to where it is now, because it’s already there. So, for that instant in time, the arrow must be stationary. But because all time is comprised entirely of instants—in every one of which the arrow must also be stationary—then the arrow must in fact be stationary the entire time. Except, of course, it isn’t.
View SolutionSubmit Solution- 1,641.9K views
- 1 answers
- 1 votes
-
To solve the puzzle read the riddle and answer the clues below to find each word. Then place the letters on the lines below. Each letter must be placed on a line marked by the same number. When all the lines are full, the answer to the riddle is revealed. Riddle: What do you get from a pampered cow?

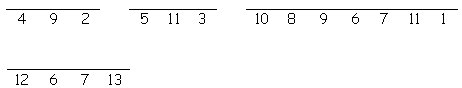
 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,639.8K views
- 1 answers
- 0 votes
-
One Saturday afternoon, four boys visited the local 5 and 10 store to buy candy. Each boy bought just his favorite candy and they all had a different favorite. They each spent under one dollar and they each bought a different amount of their favorite candy. Can you determine each boy’s full name, the type and quantity of candy each boy purchased, and how much each boy spent?
- Peter, whose last name isn’t Smythe, bought one piece less than the boy who bought the Tootsie Rolls but he spent 15 cents more.
- Adam, who spent 35 cents, spent the least. The boy who bought the lollipops spent the most.
- Tom Wilson, who spent 10 cents more than John, spent 60 cents.
- The amount spent by each boy, from the least to the most, was the boy who bought the peppermints, the boy whose last name is Smythe, the boy who bought the Tootsie Rolls, and the boy whose last name is Brown.
- Peter’s last name isn’t Parker.
- The boy who bought ten gum drops, whose last name isn’t Parker, bought the largest quantity. The boy who spent the most bought the smallest quantity.
- The boy who got seven peppermints had two more pieces than the boy who got the lollipops.
Use the grid to help solve the puzzle!
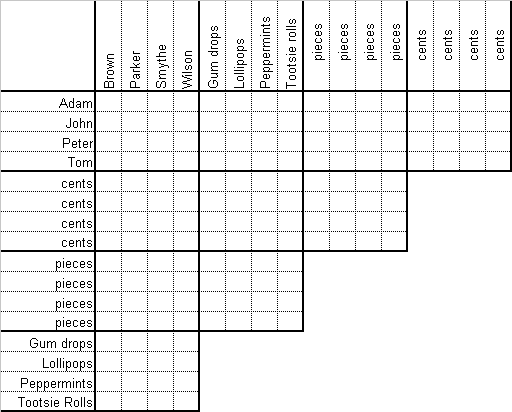 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,638.4K views
- 1 answers
- 1 votes
-
Can you find all the words in the word list in the grid below? The words can be found horizantally, vertically, diagonally, and backwords.
One day, five mothers each brought their only child to Zoo The children had a glorious time together watching the different animals and eating their favorite snacks. The kids were so good, at the end of the day each mother let her child get one item from the souvenir shop as they were leaving the zoo. Can you determine the full name of each child, each child’s favorite snack and animal, and the souvenir each brought home?
- Julia, who loves cotton candy, didn’t like the elephants. Mary didn’t get a caramel apple. The child who got the stuffed animal liked the giraffes best.
- Alan Small, the girl who liked the lions, and the child who got the activity set didn’t want to leave the zoo.
- Neither of the boys got fried dough, but one got nachos and the other one liked the monkeys best. Tom didn’t get a poster.
- The Brown child almost got a coloring book with Mary but finally decided on a poster.
- Tom, whose last name isn’t Proctor, got a toy gun but didn’t get a caramel apple. The MacGregor child had fried dough.
- Beth, who didn’t like the giraffes or the elephants best, got an activity set.
Use the grid to help solve the puzzle!
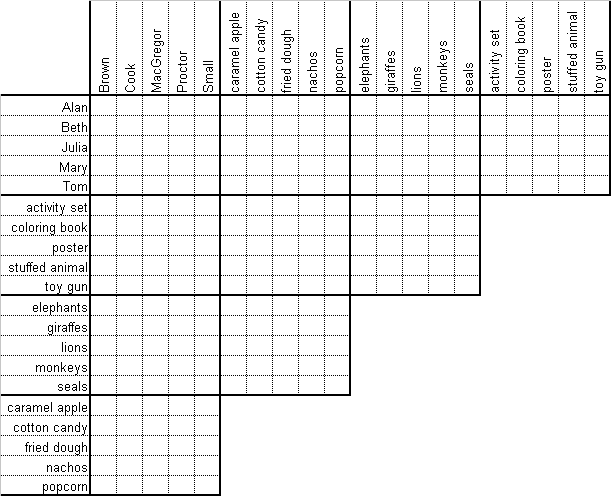 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,639.6K views
- 1 answers
- 0 votes
-

Mrs. Robinson’s 4th grade class took a field trip to the local zoo. The day was sunny and warm – a perfect day to spend at the zoo. The kids had a great time and the monkeys were voted the class favorite animal. The zoo had four monkeys – two males and two females. It was lunchtime for the monkeys and as the kids watched, each one ate a different fruit in their favorite resting place. Can you determine the name of each monkey, what kind of fruit each monkey ate, and where their favorite resting place was?
- Sam, who doesn’t like bananas, likes sitting on the grass.
- The monkey who sat on the rock ate the apple. The monkey who ate the pear didn’t sit on the tree branch.
- Anna sat by the stream but she didn’t eat the pear.
- Harriet didn’t sit on the tree branch. Mike doesn’t like oranges.
View SolutionSubmit Solution- 1,638.7K views
- 1 answers
- 1 votes
-
Five parents pick-up their children at the Puzzlefry Elementary School every Tuesday to bring the kids to their afterschool activity. Colleen and the four other children all attended a different afterschool activity and their parents always arrive at different times (between 3:00 pm and 3:30 pm). Determine each child’s full name, the first name of the parent picking them up (all the parents’ last names are the same as their child’s), the time each was picked up, and the activity each child is being brought to.
- Margie’s best friend’s mother, Mrs. Dobson, arrived before Cathy came to pick up her son. Mrs. Walsh picked up her daughter for fencing.
- Josh Steinway loved football as much as Donno liked chess, and they both liked being the last two to be picked up.
- David Holden picked up his daughter for her hiking as soon as he could, but Lynne was always there before he was.
- Margie liked being the first one picked up but she didn’t take ballet or hiking.
- Lynne’s daughter was not Margie.
- In order of their departure from school: Ann, the girl who took ballet, Mary Holden, the boy who took football, and Capri Johnson.
Use the grid to solve the puzzle!
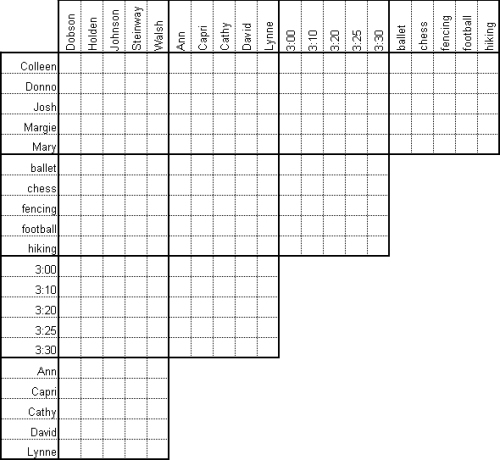 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,639.4K views
- 1 answers
- 0 votes



