For convenience sake, let’s name the balls 1-8. First we weigh {1,2,3} on the left and {4,5,6} on the right. There are three scenarios which can arise from this.

If the left side is lighter, then we know that one of 1, 2 or 3 is the lighter ball. Weigh {1} on the left and {2} on the right. By doing this, we will know if 1 or 2 is lighter. If they balance out, then 3 is the lighter one.

If the right side is lighter, then we know that either 4, 5 or 6 is the lighter ball. Weigh {4} on the left and {5} on the right. By doing this we will know if 4 or 5 is lighter. If they balance out, then 6 is the lighter one.

If {1,2,3} and {4,5,6} balance out, then we know either 7 or 8 is the lighter one. Weigh both of them to find out which one is lighter.

2 months after(+) November(11th) is January(1st)

Writing 2 in binary – 10

Now taking XOR-
10 XOR 11 = 1

Neither. The yolk is yellow. 🙂

Solution to the problem is as follows:

Answer– 533 Banana

First of all, the brute-force approach does not work. if Camel start by picking up the 1000 bananas and try to reach point B, then Camel will eat up all the 1000 bananas on the way and there will be no banana left for the Camel to return to point A.

So we have to take an approach that Camel drop the bananas in between and then return to point A, to pick bananas again.

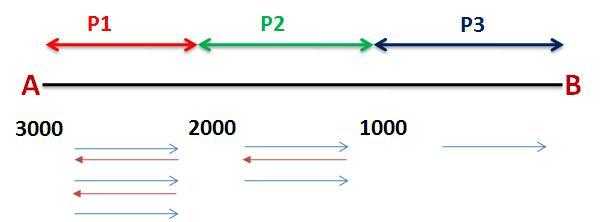
Since there are 3000 bananas and camel can only carry 1000 bananas, Camel will have to make 3 trips to carry them all to any point in between.

When bananas are reduced to 2000 then Camel can shift them to another point in 2 trips and when the number of bananas left are

In the first part, P1, to shift the bananas by 1Km Camel will have to

1. Move forward with 1000 bananas – Will eat up 1 banana in the way forward 


2. Leave 998 banana after 1 km and return with 1 banana – will eat up 1 banana in the way back


3. Pick up the next 1000 bananas and move forward – Will eat up 1 banana in the way forward 


4. Leave 998 banana after 1 km and return with 1 banana - will eat up 1 banana in the way back


5. Will carry the last 1000 bananas from point a and move forward – will eat up 1 banana

Note: After point 5 the camel does not need to return to point A again.

So to shift 3000 bananas by 1km Camel will eat up 5 bananas.

After moving to 200 km the camel would have eaten up 1000 bananas and is now left with 2000 bananas.

Hence, the length of part P1 is 200 Km.

Now in the Part P2, the Camel need to do the following to shift the Bananas by 1km.

1. Move forward with 1000 bananas - Will eat up 1 banana in the way forward


2. Leave 998 banana after 1 km and return with 1 banana - will eat up this 1 banana in the way back


3. Pick up the next 1000 bananas and move forward - Will eat up 1 banana in the way forward

Note: After point 3 the camel does not need to return to the starting point of P2.

So to shift 2000 bananas by 1km Camel will eat up 3 bananas.

After moving to 333 km the camel would have eaten up 1000 bananas and is now left with the last 1000 bananas.

The camel will actually be able to cover 333.33 km, 


I have ignored the decimal part because it will not make a difference in this example.

Hence the length of part P2 is 333 Km.

Now, for the last part, P3, the Camel only has to move forward. He has already covered 533 (200+333) out of 1000 km in Parts P1 & P2. Now he has to cover only 466 km and he has 1000 bananas.

He will eat up 466 bananas on the way forward, and at point B the Camel will be left with only 533 Bananas.

Source : http://www.ritambhara.in/camel-banana-puzzle/

We want to minimize the number of drops for the worst case, while still using an approach that works well for other scenarios. So, how can we do this? Well, we should rephrase that question and ask ourselves what is really holding us back here? The main reason why it takes such a large number of drops in the worst case with our approach above (19 drops) is because in order to test out the higher floors of the building we have to start at the lower floors of the building, and at that point we have already used a large number of drops just to get to that point.

What we should try to get with our next approach is to try to reduce the worst case scenario by trying to make all possible scenarios take the same number of drops.

What if we tried to reduce the number of drops that would be required with the linear search (with the 2nd egg) after we get to one of the higher floors? This way we counteract the fact that getting to the higher floor took so many drops, and if we use less drops for the linear search we are balancing out the worst case.

Let’s try to figure this out using some simple algebra. Suppose we drop an egg from floor x. If the egg breaks, then we would have to go through the previous x-1 floors one by one using a linear search.

But, if the egg doesn’t break, in our original algorithm we would go up x floors to find the next floor to test from. Why not just go up x-1 floors instead of x floors? This would save us 1 drop if we have to do a linear search with the 2nd egg whenever the first egg breaks – because we would be doing the linear search from floors x+1 to floor ( (x+1) + (x-1)) instead of floors x+1 to floor (x+1) + x. So, that is 1 less egg drop. This means that the next floor that should be attempted to drop from is x + (x-1) if the egg does not break from floor x. And by the same reasoning the floor after that would be x + (x-1) + (x-2) if the egg does not break on floor x + (x-1).

This would go on to form a series that looks like this:

x + (x-1) + (x-2) + (x-3) + ... + 1

The series above is what’s called a triangular series which is equal to x(x+1)/2. Because there are 100 floors in the building, we set the sum equal to 100 to solve for x:

x(x+1)/2 = 100

When the sum of the series above equals 100, we get x = 13.651, which rounds up to 14. This means that we should start from floor 14 (which is our x) and then move up x-1 (13) floors to floor 27 if the egg doesn’t break and then move up x-2 (12) floors to floor 39 and so on if the egg still does not break.

This is the number of drops required as we move up the floors in the building:

2 Eggs 100 Floors Worst Case Solution

The solution for the worst case in this scenario occurs when the threshold floor is floor number 14 – because we will drop the first egg on floor 14, and it will break. Then we have to test floors 1-13 with the 2nd egg to see where the egg breaks again, and the egg will not break on any of those floors. But since the egg broke on the floor 14, we can conclude that the threshold floor is floor number 14.