1016
points
Questions
0
Answers
201
-
We can approach this problem by realizing that we can reach any integer n by making repeated jumps of size 1, alternating between moving to the left and moving to the right. Specifically, to reach n, we can make the following jumps:
- Move 1 unit to the right
- Move 2 units to the left
- Move 3 units to the right
- Move 4 units to the left
- Move 5 units to the right
- Move 6 units to the left
- and so on, continuing to alternate directions and increasing the size of the jump by 1 each time
This sequence of jumps will eventually reach n, since the sum of the jump sizes is 1 – 2 + 3 – 4 + 5 – 6 + … = 1 + (3 – 2) + (5 – 4) + (7 – 6) + … is an infinite series that diverges to infinity.
To find the optimal solution to reach a given number n, we can first check if it is reachable by computing the sum of the first k integers, where k is the smallest positive integer such that n is less than or equal to the sum. If n is not reachable, we can stop and return “not reachable”. Otherwise, we can find the sequence of jumps as follows:
- Start at 0
- Move 1 unit to the right
- Move 2 units to the left, unless we have already reached n
- Move 3 units to the right, unless we have already reached n
- Move 4 units to the left, unless we have already reached n
- Continue alternating between left and right, increasing the jump size by 1 each time, until we reach n.
This algorithm will terminate after at most 2n steps, since the sum of the jump sizes is at most 1 + 2 + … + n = n(n+1)/2. Therefore, it provides an optimal solution to reach a given number if it is reachable.
- 3307 views
- 1 answers
- 0 votes
-
or the first question, the resulting series will converge. To see why, note that the terms that are dropped from the series are of the form 1/(n*10^k + 9), where n is a positive integer and k is a non-negative integer. We can bound each of these terms as follows:
1/(n10^k + 9) <= 1/(n10^k) = 1/n * 1/(10^k)
The series of 1/n converges by the integral test, and the series of 1/(10^k) converges to 1/9, since it is a geometric series with common ratio 1/10. Therefore, the series obtained by dropping the terms containing a 9 in the denominator is bounded above by a convergent series, and hence it also converges.
For the second question, the resulting series will still diverge. To see why, note that the terms that are dropped from the series are of the form 1/(n*10^k + 99), where n is a positive integer and k is a non-negative integer. We can write this as:
1/(n10^k + 99) = 1/(n10^k) * 1/(1 + 99/(n*10^k))
As before, the series of 1/(n10^k) converges by the integral test. However, the series of 1/(1 + 99/(n10^k)) diverges, since it is a series of terms that are greater than or equal to 1/100 for sufficiently large n. Therefore, the series obtained by dropping the terms containing two consecutive 9’s in the denominator still contains a divergent subseries, and hence it also diverges.
- 4861 views
- 1 answers
- 0 votes
-
You are correct that there seems to be an error in the footnote. Typically, when a recipe is designed for a conventional oven and you want to use a convection oven instead, you should reduce the temperature by about 25 to 30 percent, rather than a fixed amount of degrees Fahrenheit.
To illustrate, let’s say you have a recipe that calls for an oven temperature of 350°F. To convert it to a convection oven temperature, you would reduce it by 25 to 30 percent. Here’s how you can do that:
- 25% reduction: 350°F – (0.25 x 350°F) = 262.5°F
- 30% reduction: 350°F – (0.3 x 350°F) = 245°F
So, for a convection oven, you would typically reduce the temperature by 87.5°F to 105°F, depending on how much of a reduction you want to make.
Therefore, it is likely that the footnote in your cookbook should have said to reduce the temperature by 86°F if using a convection oven
- 4087 views
- 1 answers
- 0 votes
-
he probability of the sequence HH is (2/3)*(2/3) = 4/9
The probability of the sequence HT is (2/3)*(1/3) = 2/9
The probability of the sequence TH is (1/3)*(2/3) = 2/9
The probability of the sequence TT is (1/3)*(1/3) = 1/9.
So if we look on this carefully we can see that if on the first toss we get H than if we choose a combination that starts with H we have 50% chance of winning (HH is 4/9 and HT is 2/9),
and if the first toss is F and we choose a combination that starts with F we also have a 50% chance of winning (FH is 2/9 and FF is 1/9) so it seems like it doesn’t matter who picks first, but since the probability of HH is 44% and double or more that the other choices I do want to pick the sequence first.- 5639 views
- 1 answers
- 0 votes
-
If we assume that each team wins its game if it better than the opponent team then:
We don’t know which is the 2nd best team but we do know that it could loose only to the best team but we don’t know on what round. So if arrange all the teams in a tree than if the tree level up to the winner is k
than the best team played k-1 games, and to determine the 2nd best only those teams that played against the best team should play between the in the same system so we need only k-2 more games.
For example: If we have 16 teams (1-16) and each odd number is the winner and the 2nd best team is 2.
Than on the 1st round #2 is eliminated.
on the 2nd round #3 is eliminated.
on the 3rd round #5 is eliminated.
on the 4th round #9 is eliminated and #1 is the winner. k=5 so #1 played 4 games. Now the eliminated teams who played against #1 are 2,3,5,9 so 2 will play against 3 and 5 against 9 and since #2 is the 2nd best team on the next round we get #2 against #5 (or #9)
so in total we had 3 more games (k=5-2)- 5101 views
- 1 answers
- 0 votes
-
Let us assume that the player’s batting average at some point during the season was less than 80%. Let x be the number of hits the player got in the first part of the season, and y be the number of at-bats he had. Then the player’s batting average in the first part of the season is x/y, which is less than 80%.
Now, let z be the number of hits the player got in the later part of the season, and w be the number of at-bats he had in this period. Then the player’s batting average in the later part of the season is z/w, which is greater than 80%.
Let us assume that the player’s overall batting average at some point in the season was never exactly 80%. Then, the player’s overall batting average at any point in the season is the total number of hits divided by the total number of at-bats. This can be expressed as:Total batting average = (x + z)/(y + w)
Since we assumed that the player’s overall batting average was never exactly 80%, we have two cases:
Case 1: The total batting average is always less than 80%
In this case, we have: (x + z)/(y + w) < 0.8
Multiplying both sides by (y + w), we get: x + z < 0.8(y + w)
But we know that: x/y < 0.8Multiplying both sides by y, we get: x < 0.8y
Similarly, we know that: z/w > 0.8Multiplying both sides by w, we get: z > 0.8w
Adding these two inequalities, we get: x + z < 0.8y + 0.8wBut this contradicts the earlier inequality that we derived, which was: x + z < 0.8(y + w)
Therefore, case 1 cannot hold, and the total batting average must have been equal to 80% at some point in the season.Case 2: The total batting average is always greater than 80%
In this case, we have: (x + z)/(y + w) > 0.8
Multiplying both sides by (y + w), we get: x + z > 0.8(y + w)
But we know that: x/y < 0.8Multiplying both sides by y, we get: x < 0.8y
Similarly, we know that: z/w > 0.8Multiplying both sides by w, we get: z > 0.8w
Adding these two inequalities, we get: x + z > 0.8y + 0.8wThis does not contradict the earlier inequality that we derived, so case 2 can hold. In this case, there is no guarantee that the player’s batting average was ever exactly equal to any other number.
Therefore, we can conclude that the property holds only for 80%.
- 4901 views
- 1 answers
- 0 votes
-
draw a vertical line from the right bottom of the L-shape and a horizontal line from the left top of the L-shape do that this two lines meet each other.
This gives us 3 squares: the right lower part of the L-shape (lets call it rectangle C), The vertical rectangle of the L-shape (lets call it rectangle B), and the new rectangle between them (let call it rectangle A).
Since Any line passing through the center of a rectangle divides it in half we find the center of rectangle A by drawing the intersecting diagonals.
We do the same for the square made up from the 3 rectangles (A,,B,C), and so the line passing threw 2 two points divides the L-shape into 2 equal parts.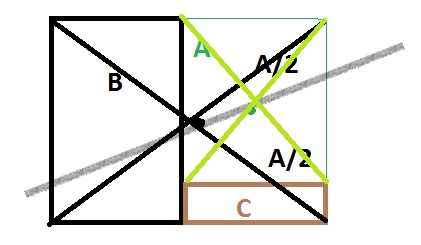
- 6986 views
- 1 answers
- 0 votes
-
If all the cards are initially red, the first player can always win the game.
To see why, note that the game can be divided into rounds, where each round consists of both players making a move. The first player will always start each round, and the second player will always finish each round.
In the first round, the first player can select the left-most 50 cards and flip them, which will leave the left-most 50 cards blue and the remaining 1964 cards red. In subsequent rounds, the first player can always choose the left-most 50 red cards, because there will always be at least 50 red cards to the left of any blue card. By doing this, the first player will always ensure that there are at least 50 consecutive red cards at the left end of the table, which means that the game can continue.
Eventually, the first player will flip the left-most 50 red cards and win the game, because there will be no more red cards left and the second player will not be able to make a move.
Therefore, the first player can always win the game if all the cards are initially red, and it is preferable to be the first player to make the first move.
- 4520 views
- 1 answers
- 0 votes
-
We can determine the coefficients of the polynomial by making evaluations of the polynomial at specific values.
First, we can evaluate the polynomial at x = 0. This will give us the constant term of the polynomial.
Next, we can evaluate the polynomial at x = 1. This will give us the sum of all the coefficients.
Then, we can evaluate the polynomial at x = 2. This will give us the sum of the squares of all the coefficients.
We can continue this process and evaluate the polynomial at x = 3, x = 4, and so on, until we have enough equations to solve for all the coefficients.
Specifically, if the degree of the polynomial is n, we can evaluate the polynomial at n + 1 distinct values of x to obtain a system of n + 1 linear equations in n + 1 unknowns (the coefficients of the polynomial). We can then solve this system of equations to determine the values of the coefficients.
Therefore, we need to call the evaluation function at least n + 1 times to identify the polynomial. Note that this is a lower bound, and in practice, we may need to call the evaluation function more than n + 1 times to ensure that we have enough independent equations to solve for all the coefficients.
- 5472 views
- 1 answers
- 0 votes
-
In this game, the outcomes of the coin flips are independent, which means that the result of one flip does not affect the outcome of the other flip. Therefore, each player has a 50-50 chance of correctly guessing the other player’s coin.
If both players guess randomly, the probability of both players guessing correctly is (1/2) x (1/2) = 1/4, and the probability of at least one player guessing incorrectly is 1 – 1/4 = 3/4.
Therefore, on average, for every 4 rounds played, the team will win 2 Euros once and lose 1 Euro three times, resulting in a net loss of 1 Euro for every 4 rounds. This means that over the long run, the team will lose money and the third person will make a profit.
So, if your objective is to win money, you would be better off trading places with the third person.
- 4592 views
- 1 answers
- 0 votes

