147
points
Questions
4
Answers
14
-
- 8977 views
- 1 answers
- 0 votes
-
The Answer is quite Funny:

- 5129 views
- 1 answers
- 0 votes
-
Just One!
example
If u get Blue rock with label as “blue+red” => this is red as all labels are wrong.
In this way u can logically solve this puzzle.- 8315 views
- 2 answers
- 0 votes
-
If We Cut Like this we will get a solution like:
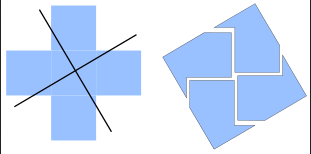
- 7208 views
- 1 answers
- 0 votes
-
The person standing at the back of the line can see all the people. I think it is important to consider that this problem has specifically 100 people in it, instead of some variable amount. This means the person in the back can see 99 people in blue and red hats in front of him. Since there are an odd number of hats the last person can see, it means that:
1. The number of red and blue hats the last person can see is not equal.
2. Either the red or the blue hats contain an odd number of hats, but not both.
With this in mind, we will be able to consistently communicate hat colors to all the participants. The person in the back of the line will begin by counting all the hats, and saying whatever color has an odd number of hats. The second person will then be able to count the hats in front of him (meaning all hats the last person saw minus the one he is wearing) if he sees an even number of the same color the first person said, he must be wearing that colored hat, otherwise he is wearing the other colored hat.
For example, if the person in the back sees an odd number of red hats, he will declare “red”. The second to last person will then count the amount of red hats he sees, if he sees an odd number, it means he is wearing a blue hat, if he sees an even number, it means he is wearing a red hat.
This process will work if every person in line keeps track of which colors have an odd or even count. Thus the worst case for this solution is 99, since the person at the front will answer solely based on what is in front of him, he will have a 50% chance of guessing correctly.
- 45069 views
- 1 answers
- 2 votes
-
Reserve one prisoner with a special assignment (I’ll call her Sam). Each prisoner will turn on the light once, and only once, sending a signal to Sam. When Sam receives it, he notes that a signal has been received, and turns the light off. Once 99 signals are received, Sam knows that everybody has been in the room. Thus the instructions for each prisoner are:
- If you enter the room with the light off, and you have never turned it on, then turn it on.
- Otherwise, leave it.
- 5423 views
- 1 answers
- 0 votes
-
There are 3 types of configuration possible:
(a) all coins have same face up
(b) 3 coins have same face up (and 1 has the other face up)
(c) 2 coins have same face up (and other 2 have the other face up)Config (a) is the desired final position. Configs (b) and (c) arepotentially one step away from the final position F (where all coins have same side facing up). However, is there a config such that we can choose one of O, S or D and then we are guaranteed to reach the final desired position F ? Yes, there is. A special case of config (c) where the diagonally opposite coins have same face up is such a penultimate position:
H T T H
T H or H T
Applying the D operation here will definitely result in F.Perhaps our goal then should be to reach this position F’ from other positions.
If two coins along a side have same face up, then F can be reached through F’ by the following sequence: S, D.
Therefore, F can be reached from config (c) by the following sequence:D, S, D.If a single coin is face up, then we have the following sequence towards F: O, D, S, D.
Applying this sequence to config (b) will definitely lead to F. Applying this sequence to config (c) however might result in config (b). Therefore this sequence must be repeated:
O, D, S, D, O, D, S, D.This is the desired sequence of operations which will guarantee that the final position F is reached at some time during its execution.
- 8953 views
- 2 answers
- 0 votes
-
Suppose that point i has angle 0 (angle is arbitrary in this problem) — essentially this is the event that point i is the “first” or “leading” point in the semicircle. Then we want the event that all of the points are in the same semicircle — i.e., that the remaining points end up all in the upper halfplane.
That’s a coin-flip for each remaining point, so you end up with 1/2n−1. There’s n points, and the event that any point i is the “leading” point is disjoint from the event that any other point j is, so the final probability is n/2n−1 (i.e. we can just add them up).
A simple check for this answer is to notice that if you have either one or two points, then the probability must be 1, which is true in both cases.
- 6534 views
- 1 answers
- 0 votes
-
Suppose that there are N wires.
If N is even: At the first end, connect pairs of wires together,
leaving two wires unconnected. Go to the other end. Find a pair of
connected wires, and number them #2 and #3. Find another pair and
label them #4 and #5. Repeat for all of the pairs, with the last pair
labeled #N-2 and #N-1. There remains two wires that are not connected
to each other. Label one of these #1 and the other #N. Connect #1 to
#2, #3 to #4, etc, leaving #N-1 and #N unconnected. Go back to the
first end. One of the originally unconnected wires still is
unconnected. Label it #N and label the other originally unconnected
wire #1. Now find the wire connected to #1 and label it #2. The wire
that originally was connected with new wire #2 can be labeled #3. The
wire that is now connected to the newly labeled #3 is #4. In this way,
all of the wires
can be identified on both ends in two trips (one round trip).If N is odd: At the first end, connect pairs of wires together,
leaving one wire unconnected. Label it #1. Go to the other end. Find a
pair of connected wires, and number them #2 and #3. Find another pair
and label them #4 and #5. Repeat for all of the pairs, with the last
pair labeled #N-1 and #N. There remains one wire that is not connected
to any other wire. Label it #1. Connect #1 to #2, #3 to #4, etc,
leaving #N unconnected. Go back to the first end. Find the wire
connected to #1 and label it #2. The wire that originally was
connected with new wire #2 can be labeled #3. The wire that is now
connected to the newly labeled #3 is #4. In this way, all of the wires
can be identified on both ends in two trips (one round trip).- 7231 views
- 1 answers
- 0 votes
-
Initial Thoughts:
Initially, this problem seems very intimidating because the idea that any four cards could be “encoded” to reveal another card is a bit crazy. One of the first things, I realized was that since you have 5 cards and there are 4 distinct suits, each hand will have at least one duplicate suit.
In order to obtain the value of the card, I thought I could use the 4 spots in indicate a 4-bit number, this would give us all numbers up to 15! Since we only needed numbers 1-13, I thought this was a really good option, however I couldn’t find a way to give my partner the suit of the hidden card with this option.
The Main Solution:
My solution ended up being a modification of my Initial Thoughts. Since there is always at least one duplicate suit in a hand of 5, I will always choose a card that has a corresponding duplicate suit for the face down card, and the card with the same suit will go in the “0” position.
In order to obtain the value of the card, we can only use the last 3 spots, so with our original thought of using base 2, we can communicate numbers 1-7.
We always have three cards is spots “1”, “2”, and “3”, so the rule I came up with involves assigning “1”‘s to spots where the current card is greater than the card preceding it, and “0” otherwise Let’s say we have cards 1, 2, 3 ordered by rank.
If we wanted to display the value 3, our card order would be 231.
- 2 is in the “one” position and has no preceding number, so we will look at the number in the “three” position, and see that 2 is greater than 1, so our string is “1”.
- 3 is in the “two” position and is greater than 2, which is in the “one” position, so our string is “11”
- 1 is in the “three” position and is less than 3, which is in the “two” position, so our final string is “110”.
110 is binary for 3, so we have just represented the value of 3 to our partner.
How could we show if the value of the hidden card was 8 or greater?
The answer is: We don’t need to. Since there are 13 values in a deck, the difference between any two cards will always be 6 or less.
You may be thinking, well what about 2 and K?! The difference between these two cards is 11! True, if you go from 2 -> K. But if you go from K -> 2, the difference is only 2! (K-> A -> 2). This means that it is important that the first face up card you pick has an absolute difference of 6 or less from the last card you pick, along with the same suit. Any two card values will always have one.
For example: If you have 2♠, 9♠, K♦, 3♥, A♣. You would hand the dealer the cards in this order: 9♠, 3♥, K♦, A♣, 2♠(face down). My partner would see that that suit is ♠. Using the base 2 pattern on (3♥, K♦, A♣), we can get the value “011” which is 6. By adding our value 6 to 9♠ we see that we get 2 (9 -> 10 -> J -> Q -> K -> A -> 2). Thus our face down card is the 2♠, and my partner and I have stumped the dealer.
In this situation we assume that A is the highest of the the values, but this can always be changed around.
You might be wondering what we would do if we had duplicate value of the card. What if our hand was 5♠, 10♠, 5♦, 5♥, 5♣ ?!
We got 4 cards with all the same value! The simple solution to this is to create a suit ordering. My personal preference is ♣(clubs), ♠(spades), ♥(hearts), ♦ (diamonds), but you and your partner can choose any order you want.
So, we would hand the dealer the cards in this order: 5♠, 5♦, 5♣,5♥,10♠(face down). So we would see that our starting suit is ♠, and starting value is 5. (5♦, 5♣,5♥) will translate to “101” because (♥ < ♦) , (♦ > ♣), and (♣ < ♥), and we have communicated the value of 5. So we add 5 to our starting value and see our answer is 10♠. Sorry dealer, no tricks with our plan.
Here we can ignore the values and look only at the suits since they are all the same.
This works because a deck of 52 cards has no duplicates, so the deck has an exact ordering.
- 9124 views
- 1 answers
- 0 votes

