My First Thought About this question was:
It is obvious that the anchor in this problem plays a key role, and that the anchor is also a node, say a,  that has an integer value, v(a), associated with it. Since the graph is connected this means that from any node n, there exists a path to any other node m. We are also unable to determine the order of the sequence of operations.

but finally i got the solution:

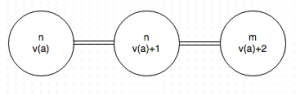
Since this graph is connected, we know there is at least one node that shares an edge with the anchor, or at least one node is a direct neighbor to the anchor.

For example: Say the connected undirected graph has 3 nodes.

OP() will be called some finite amount of times. This will continue until all direct neighbors of the anchor are equal to v(a)+1. After this, OP() will be called another finite amount of times. Eventually, the value any given node n, becomes equal to v(a) + d, where d is the length of shortest path from n to a.

At this point, any operation on a node in the graph would result in an unchanged v(n). Thus, the graph is stabilized and this has taken place in a finite amount of steps.

For my example, I used a graph with only 3 nodes, but you can easily see how this effect would take place on a much larger graph. The key here is that the graph is connected, so all nodes have at least one path to the anchor.

This sentence was made on 1st January.
Mr Puzzel’s birthday is on 31st December.  He was 17 the day before yesterday.
He was 18 yesterday.
He will be 19 this year, and 20 next year!

Example –
Birthday on 31 Dec 2010.   Statement made on 1st January 2011.
on 30th Dec 2010 – Mr Puzzle is 17 Yrs Old
on 31th Dec 2010 – Mr Puzzle is 18 Yrs Old
on 1st Jan 2011 – Mr Puzzle is 17 Yrs Old but in this year only on 31th Dec 2011 – He will be 19yrs Old
Next year – on 31th Dec 2012 – He will be 20yrs Old

This can be the simplest answer for this question:

If the King asks all three men the same question, “Are you the Commoner?”, he will receive one of two possibilities of answers. Either {Yes, No, No} or {Yes, Yes, No} or any permutation of the two. This is because the Knight will always answer “No”, the Knave will always answer “Yes”, and the Commoner will answer either “Yes” or “No”.

At this point, the king only has the choose the unique answer in the set of answers he receives. If the answer was {Yes, Yes, No}, he will choose the man who answered “No” and his daughter will marry the Knight, if it was {Yes, No, No}, he would choose the man who answered “Yes” and his daughter would marry the Knave. Regardless, with this strategy, his daughter would never have to marry a commoner and the kingdom would be safe once again.

Answer To The follow-up Question

Think of each of the the three as A, B, and C.

If we ask A and C, “Does B ever lie?”. We will receive 3 possibilities of answers { Yes, Yes}, {Yes, No}, or {No, Yes}. Notice we will never get {No, No}. This is because A and C could be:

• Commoner and the Knight, meaning the Knight will Answer “Yes”
• Commoner and the Knave, meaning the Knave will Answer “Yes”
• Knight and the Knave, meaning they will never agree.

If the King receives {Yes,Yes} from A and C, he should choose B.

If the King receives {Yes, No} or {No, Yes}, he should choose the man who answered “Yes”.

Total 7 races are required

Draw out a table

In problems like this, it helps tremendously to create some sort of visual aid that you can refer to. With that in mind, we have created this table where each entry represents a different horse.

X1   X2   X3   X4   X5 

X6   X7   X8   X9   X10 

X11 X12 X13 X14 X15 

X16 X17 X18 X19 X20 

X21 X22 X23 X24 X25 

Let’s say that we have 5 races of 5 horses each, so each row in the table above represents a race. So, “X1 X2 X3 X4 X5 ” represents a race, and “X6 X7 X8 X9 X10 ” represents another race, etc. In each row, the fastest horses are listed in descending order, from the fastest (extreme left) to the slowest (extreme right). The fastest horses in each race are the ones on the left – so in the first race X1 was the fastest and X5 was the slowest. In the second race X6 was the fastest, X7 was the second fastest and so on.

Only 5 horses each race

So, now we ask ourselves: what do we know after these 5 races? Well, we do have the 5 five fastest horses from each race (X1, X6, X11, X16, and X21). But, does that mean we have the 5 fastest horses? Think about that for a second. Well, actually it does not mean that we have the 5 fastest horses. Because, what if the 5 fastest horses just happened to be in the first race – so X1 X2 X3 X4 X5 are the fastest horses. X1, X6, X11, X16, and X21 are all the fastest horses in their individual groups, but there could be one group that just happened to have all of the fastest horses. Remember we haven’t compared all the horses to each other since we can only run 5 horses in a race, so that is still a possibility. This is very important to understand in this problem.

Work through a process of elimination

Well, now that we’ve had 5 different races, we can eliminate the slowest 2 horses in each group since those horses are definitely not in the top 3. This would leave these horses:

X1   X2   X3   

X6   X7   X8   

X11 X12 X13 

X16 X17 X18  

X21 X22 X23 

We also know the 5 fastest horses from each group – but it’s important to remember that the 5 group leaders are not necessarily the 5 fastest horses. So what can we do with that information?
Well, we can race those 5 horses against each other (X1, X6, X11, X16, and X21) and that would be the 6th race. Let’s say that the 3 fastest in that group are X1, X6, and X11 – automatically we can eliminate X16 and X21 since those 2 are definitely not in the top 3.

What other horses can we eliminate after this 6th race? Well, we can automatically eliminate all the horses that X16 and X21 competed against in the preliminary races – since X16 and X21 are not in the top 3 then we also know that any horse that’s slower than those 2 is definitely not in the top 3 either. This means we can eliminate X17 X18 X22 and X23 along with X16 and X21.

Now, we also know that X1 is the fastest horse in the group since he was the fastest horse out of the 5 group leaders. So, we don’t need to race X1 anymore. Are there any other horses that we can eliminate from further races? Well, actually there are. Think about it – if X6 and X11 are the 2nd and 3rd fastest in the group leaders, then we should be able to eliminate X8 since X6 raced against him and he was in 3rd place in that race. X7 could only possibly be the 3rd fastest, and since X8 is slower than X7, we can safely eliminate X8. We can also eliminate X12 and X13 since X11 was the 3rd fastest in the group leaders, and X12 and X13 were slower than X11.
So, all together we can eliminate these horses after the 6th race: X17 X18 X22 X23 X16 X21, X12, X13, X8 and X1. This leaves us with the following horses to determine the 2nd and 3rd fastest horses:

X2   X3   

X6   X7   

X11 

What is the solution?

This means we only have 5 horses left! Now we race those horses one more time – in the seventh (7th) race – and we can take out the top 2 horses and that would mean we have the 2nd and 3rd place horses! So, we have found our answer! It takes 7 races to find the top 3 horses in this problem.