Assuming,1. The dissolved Pills can be used next day.

Add one more A pill to the glass and let it dissolve.

Take half of the water today and half tomorrow.

So, Percentage of Pill A and Pill B on both the day in overall be managed equal

Player 1 picks the first coin from right end and player 2 picks coin which have higher value from either end in next step player 1 can continue to pick up higher value coin from either end

The first player loses iff n=6k+1

If n=1, the first player is forced to take it and hence loses. Now that we have identified a losing position, it makes sense to send the opponent to the losing position. Hence if n=2,3,4,5 or 6, the first player can take away n-1 coins and give just 1 coin to the opponent, forcing them to lose.

If n=7, anything that the first player does, the opponent is going to end up with 2,3,4,5 or 6 coins. But as explained earlier, the opponent can then take away the required number of coins to give a single coin to the first player, forcing them to lose. Thus n=7 is a losing position, from which it follows that n=8,9,10,11 and 12 are winning positions.

By induction, it can be proved that numbers of the form 6k+1 are the losing positions. In general, in an impartial game that is acyclic and guaranteed to end in a win for one player, here is the procedure to find out which states are winning positions for the first player. Suppose that there is a property P that you can assign to some of the game states such that:

1. The ultimate losing state satisfies the property P
2. From a state that satisfies P, it is impossible to move to another state that satisfies P
3. From any state that does not satisfy P, it is possible to move to some state that satisfies P

In such a case, the P states are exactly the losing states.

For this problem, let us define the property P for states (integers for us) as n leaves remainder 1 on division by 6. Then it is easy to see that:

1. The ultimate losing state (1) satisfies P
2. From a number that is 1 modulo 6, it is impossible to obtain another one by subtracting 1,2,3,4 or 5. That is, We cannot move from a P state to another
3. From a number that is 0,2,3,4 or 5 modulo 6, we can subtract 5,1,2,3 and 4 respectively to obtain a number which is 1 modulo 6. That is, from any non-P state, we can move to a P-state

Hence the only losing states are those with integers that are 1 modulo 6.

with 7 nodes on the left (boys) and 6 nodes on the right (girls).
There are 7*6=42 edges.
The 7 nodes on the left have degree 6 and the 6 nodes on the right have degree 7

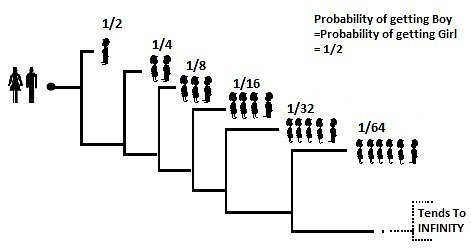
Total Probability =ΣProbability of event  = 1/2 +1/4 +1/8 + …= 1

Now,
Expected no of Boys will be
= Σ Probability of event x Number of Boys in that event
=1/2 x1  + 1/4 x1  + 1/8 x 1  +  ….
= 1/2+1/4+1/8+1/16+…
= 1
Expected no of Girls will be
= Σ Probability of event x Number of Girls in that event
=1/2 x0  + 1/4 x1  + 1/8 x 2  + 1/16 x 3  ….         (See tree diagram)
= 1/4+ 2/8 + 3/16+ 4/32 …
=Sn
Sn          =     1/4+ 2/8 + 3/16+ 4/32  +…
1/2x Sn   =            1/8 + 2/16 + 3/32+ 4/64 +…   (Shifting all terms to right)
————————————————————-
Sn/2        =    1/4+ 1/8+ 1/16 + 1/32 +…              (Subtracting)

Sn/2 =  1/4 x 2
Sn = 1/4 x 2 x 2 =1

Expected no of Girls will be =1

Therefore
Ratio of no of Boys to Girls =
Expected no of Boys    = 1   = 1:1
Expected no of Girls       1

SWITCHING will be more advantageous,

Switching will make winning probability to 2/3 and staying will have probability 1/3
_______________________________________________________________________________________

Assume that you always start by picking Door #1, and the host then always shows you some other door which does not contain the car, and you then always switch to the remaining door.If the car is behind Door #1, then after you pick Door #1, the host will open another door (either #2 or #3), and you will then switch to the remaining door (either #3 or #2), thus LOSING.

If the car is behind Door #2, then after you pick Door #1, the host will be forced to open Door #3, and you will then switch to Door #2, thus WINNING.

If the car is behind Door #3, then after you pick Door #1, the host will be forced to open Door #2, and you will then switch to Door #3, thus WINNING.

Hence, in 2 of the 3 (equally-likely) possibilities, you will win. Ergo, the probability of winning by switching is 2/3.

Choose an explanation to the Monty Hall Problem:

1/3 vs 2/3 – Solution #1 to the Monty Hall Problem

There is a 1/3 chance of the car being behind door number 1 and a 2/3 chance that the car isn’t behind door number 1. After Monty Hall opens door number 2 to reveal a goat, there’s still a 1/3 chance that the car is behind door number 1 and a 2/3 chance that the car isn’t behind door number 1. A 2/3 chance that the car isn’t behind door number 1 is a 2/3 chance that the car is behind door number 3.

100 Doors! – Solution #2 to the Monty Hall Problem

Imagine that instead of 3 doors, there are 100. All of them have goats except one, which has the car. You choose a door, say, door number 23. At this point, Monty Hall opens all of the other doors except one and gives you the offer to switch to the other door. Would you switch? Now you may arrogantly think, “Well, maybe I actually picked the correct door on my first guess.” But what’s the probability that that happened? 1/100. There’s a 99% chance that the car isn’t behind the door that you picked. And if it’s not behind the door that you picked, it must be behind the last door that Monty left for you. In other words, Monty has helped you by leaving one door for you to switch to, that has a 99% chance of having the car behind it. So in this case, if you were to switch, you would have a 99% chance of winning the car.

Pick a Goat – Solution #3 to the Monty Hall Problem

To win using the stay strategy, you need to choose the car on your first pick because you’re planning to stay with your initial choice. The chance of picking the car on your first pick is clearly one out of three. But, in order to win using the switch strategy, you only need to pick a goat on your first pick because the host will reveal the other goat and you’ll end up switching to the car. So you want to use the strategy that lets you win if you choose a goat initially because you’re twice as likely to start by picking a goat.

Scenarios – Solution #4 to the Monty Hall Problem

To understand why it’s better to switch doors, let’s play out a few scenarios. Let’s see what will happen if you were to always stay with your original choice. We’ll play out three scenarios, one for each door that the car could be behind (door number 1, door number 2, or door number 3). And it doesn’t matter which door you start out with, so, to keep it simple, we’ll always start by choosing door number 1.Stay strategy, scenario 1: the car is behind door number 1. You choose door number 1, then the host reveals a goat behind door number 2 and because you always stay, you stay with door number 1. You win the car! Stay strategy, scenario 2: the car is behind door number 2. You start by picking door number 1, the host reveals a goat behind door number 3, and you’re using the stay strategy so you stay with door number 1. You get a goat and don’t win the car. Stay strategy, scenario 3: the car is behind door number 3. You pick door number 1, the host opens door number 2 to reveal a goat, you stay with door number 1, and you get a goat. So, using the stay strategy, you won the car one out of three times. That means that in any one instance of playing the game, your chance of winning the car if you choose to stay is 1/3 or about 33%.

Now let’s try switching doors. Again, we’ll always start by picking door number 1. Switch strategy, scenario 1: the car is behind door number 1. You choose door number 1, the host opens door number 2 to reveal a goat, you are using the switch strategy so you switch to door number 3. You get a goat. Switch strategy, scenario 2: the car is behind door number 2. You start by picking door number 1, the host opens door number 3 to reveal a goat, you switch to door number 2 and win the car! Switch strategy, scenario 3: the car is behind door number 3. You pick door number 1, the host opens door number 2 to reveal a goat, you switch to door number 3 and win the car again! So, with the switch strategy you won the car 2 out of 3 times. That means, that in any one instance of the game, your chance of winning the car if you choose to switch doors is 2/3 or about 67%.

Therefore, if you play the game three times and stay, on average you’ll win the car once. But if you play the game three times and switch each time, on average you’ll win the car twice. That’s twice as many cars!

0%

Explanation:
1) Why can’t be 1/4 :
If the answer is 1/4, then as we know two out of four answer choices is ‘1/4’, the answer has be 1/2.
This is a contradiction, so the answer cannot be 1/4.

2) why cant be 1/2 :
If the answer is 1/2 then because answer:”1/2″ is 1 out of 4 answer choices, the answer must be 1/4. This is also a contradiction. So the answer cannot be 1/2.

3) why cant be 1 :
If the answer is 1 then because answer:”1″ is 1 out of 4 answer choices, the answer must be 1/4. Again the same contradiction and therefore answer cannot be 1.

Birbal will Ask him to pay rent for keeping his water in his well 
OR
Take out all the water from the well,

We light rope A from one end and rope B from both ends simultaneously.
When rope B is fully burned (it means that half an hour is passed and rope A has only one hour left) we light the other end of rope A immediately and of course start cooking the egg.
When rope A is fully burned (it means that fifteen minutes is passed from the time we started cooking the egg) your meal is ready…! 😉

So I first solved it through a recursive function. (I still don’t know why I did this stupid thing). So small-input file gave correct results but the program terminated during large-input evaluation (stack overflow error). :O

Here is the code (recursive):

import java.io.*;
import java.util.*;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class cookie {
 static int i = 0;
 static Vector<Double> vec;
 static double target=0;
 static double fRate = 0;
 static double fCost = 0;
 public static double fun(double prevFarmBuyTimes, double rate){
 if(i==0){
 vec.add(target/rate);
 }
 double farmTime = prevFarmBuyTimes+fCost/rate;
 rate+=fRate;
 double WaitingTime = target/rate;
 double projection = farmTime+WaitingTime;
 vec.add(projection);
 i++;
 if(vec.elementAt(i-1)>vec.elementAt(i)){
 return fun(farmTime, rate);
 }
 else
 {
 return vec.elementAt(i-1);
 }
 }
 public static void main(String[] args) throws Exception{
 BufferedReader br = new BufferedReader(new FileReader("d:\\B-large-practice.in"));
 BufferedWriter bw = new BufferedWriter(new FileWriter("d:\\result.txt"));
 int ncases = Integer.parseInt(br.readLine());
 int index = 1;
 while(index<=ncases){
 Pattern p = Pattern.compile("\\d+.\\d+");
 Matcher m = p.matcher(br.readLine());
 if (m.find())
 fCost = Double.parseDouble(m.group());
 if (m.find())
 fRate = Double.parseDouble(m.group());
 if (m.find())
 target = Double.parseDouble(m.group());
 //LOGIC STARTS HERE
 vec = new Vector<Double>();
 i=0;
 double time = fun(0,2);
 bw.write("Case #"+index+": "+time);
 bw.newLine();
 bw.flush();
 System.out.println(time);
 index++;
 } 
 } 
}

And here is the improved version without recursion.(Gives correct results for large-inputs):

import java.io.*;
import java.util.*;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class cookie {
 public static void main(String[] args) throws Exception{
 BufferedReader br = new BufferedReader(new FileReader("d:\\B-large-practice.in"));
 BufferedWriter bw = new BufferedWriter(new FileWriter("d:\\result.txt"));
 int ncases = Integer.parseInt(br.readLine());
 int index = 1;
 int i = 0;
 Vector<Double> vec;
 double target=0;
 double fRate = 0;
 double fCost = 0;
 while(index<=ncases){
 Pattern p = Pattern.compile("\\d+.\\d+");
 Matcher m = p.matcher(br.readLine());
 if (m.find())
 fCost = Double.parseDouble(m.group());
 if (m.find())
 fRate = Double.parseDouble(m.group());
 if (m.find())
 target = Double.parseDouble(m.group());
 vec = new Vector<Double>();
 i=0;
 double rate =2;
 vec.add(target/rate);
 double result = 0;
 double prevFarmBuyTimes=0;
 while(true){
 double farmTime = prevFarmBuyTimes+fCost/rate;
 prevFarmBuyTimes=farmTime;
 rate+=fRate;
 double WaitingTime = target/rate;
 double projection = farmTime+WaitingTime;
 i++;
 vec.add(projection);
 if(vec.elementAt(i-1)<vec.elementAt(i)){
 result = vec.elementAt(i-1);
 break;
 }
 }
 System.out.println(result);
 bw.write("Case #"+index+": "+result);
 bw.newLine();
 bw.flush();
 index++;
 } 
 } 
}