Brain Teasers & Puzzles
-
- 1,646.4K views
- 1 answers
- 1 votes
-
- 1,666.4K views
- 4 answers
- -1 votes
-
Answer the clues below to find each word. Then place the letters on the lines below. Each letter must be placed on a line marked by the same number. When all the lines are full, our Happy New Year greeting will be revealed. 
a greeting .. 
bits of falling shredded paper .. 
to call forth .. 
goals made for the New Year .. 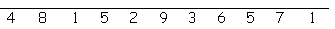
you blow these at festive gatherings .. 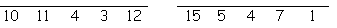
traditional New Year’s song .. 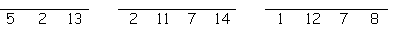
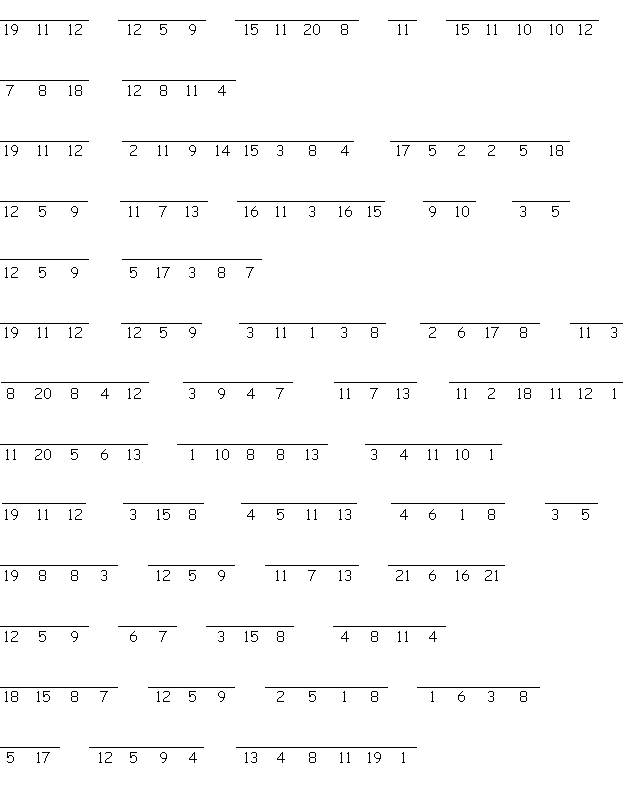 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,639.5K views
- 1 answers
- 0 votes
-
A king has a daughter and wants to choose the man she will marry. There are three suitors from whom to choose, a Knight, a Knave, and a Commoner. The king wants to avoid choosing the Commoner as the bridegroom, but he does not know which man is which. All the king knows is that the Knight always speaks the truth, the Knave always lies, and the Commoner can do either. The king will ask each man one yes/no question, and will then choose who gets to marry the princess. What question should the king ask and how should he choose the bridegroom?
A followup question:
Suppose the three suitors know each other (an assumption that’s not needed in the original problem). Then find a new strategy for the king where the king only needs to ask a question of any two of the three suitors in order to pick the bridegroom.
View SolutionSubmit Solution- 1,645.2K views
- 1 answers
- 0 votes
-
In this problem, you and a partner are to come up with a scheme for communicating the value of a hidden card. The game is played as follows:
- Your partner is sent out of the room.
- A dealer hands you 5 cards from a standard 52 card deck.
- You look at the cards, and hand them back to the dealer, one by one, in whatever order you choose.
- The dealer takes the first card that you hand her and places it, face up, in a spot labeled “0”‘. The next three cards that you hand her, she places, similarly, in spots labeled “1”, “2”, and “3”. The last card that you hand her goes, face down, in a spot labeled “hidden”. (While you control the order of the cards, you have no control over their orientations, sitting in their spots; so you can’t use orientation to transmit information to your partner.)
- Your partner enters the room, looks at the four face-up cards and the spots in which they lie and, from that information (and your previously-agreed-upon game plan), determines the suit and value of the hidden card.
Question: What is the foolproof scheme that you and your partner settled on ahead of time?
As a follow-up question, consider the same problem but with a 124-card deck.
View SolutionSubmit Solution- 1,643.7K views
- 1 answers
- 0 votes
-
You’re an electrician working at a mountain. There are N wires running from one side of the mountain to the other. The problem is that the wires are not labeled, so you just see N wire ends on each side of the mountain. Your job is to match these ends (say, by labeling the two ends of each
wire in the same way).In order to figure out the matching, you can twist together wire ends, thus electrically connecting the wires. You can twist as many wire ends as you want, into as many clusters as you want, at the side of the mountain where you happen to be at the time. You can also untwist the wire ends at the side of the mountain where you’re at. You are equipped with an Ohm meter, which lets you test the connectivity of any pair of wires. (Actually, it’s an abstract Ohm meter, in that it only tells you whether or not two things are connected, not the exact resistance.)
You are not charged [no pun intended] for twisting, untwisting, and using the Ohm meter. You are only charged for each helicopter ride you make from one side of the mountain to the other. What is the best way to match the wires? (Oh, N>2, for there is no solution when N=2.)
View SolutionSubmit Solution- 1,641.8K views
- 1 answers
- 0 votes
-
Given N points randomly distributed around the circumference of a circle, what is the probability that all N points lie on the same semi-circle?
View SolutionSubmit Solution- 1,641.1K views
- 1 answers
- 0 votes
-
In a finite, undirected, connected graph, an integer variable v(n) is associated with each node n. One node is distinguished as the anchor. An operation OP(n) is defined on nodes:
OP(n):
if node n is the anchor, then do nothing,
else set v(n) to the value 1 + min{v(m)}, where m ranges over all neighbors of n that are distinct from n.An infinite sequence of operations <OP(n),OP(m), …> is executed, the node arguments n, m, … for the operations being chosen arbitrarily and not necessarily fairly. Show that eventually all v(n) stabilize. That is, that after some finite prefix of the infinite sequence of operations, no further operation changes v(n) for any node n.
View SolutionSubmit Solution- 1,640.9K views
- 1 answers
- 0 votes
-
A square table has a coin at each corner. Design an execution sequence, each of whose steps consists of one of the following operations:
- ONE: The operation chooses a coin (possibly a different one with each execution of the operation) and flips it.
- SIDE: The operation chooses a side of the table and flips the two coins along that side.
- DIAG: The operation chooses a diagonal of the table and flips the two coins along that diagonal.
such that at some point during the execution (not necessarily at the end), a state where all coins are turned the same way (all heads or all tails) obtains.
View SolutionSubmit Solution- 1,643.5K views
- 2 answers
- 0 votes
-
N prisoners get together to decide on a strategy. Then, each prisoner is taken to his own isolated cell. A prison guard goes to a cell and takes its prisoner to a room where there is a switch. The switch can either be up or down. The prisoner is allowed to inspect the state of the switch and then has the option of flicking the switch. The prisoner is then taken back to his cell. The prison guard repeats this process infinitely often, each time choosing fairly among the prisoners. That is, the prison guard will choose each prisoner infinitely often.
At any time, any prisoner can exclaim “Now, every prisoner has been in the room with the switch”. If, at that time, the statement is correct, all prisoners are set free; if the statement is not correct, all prisoners are immediately executed. What strategy should the prisoners use to ensure their eventual freedom?
(Just in case there’s any confusion: The initial state of the switch is unknown to the prisoners. The state of the switch is changed only by the prisoners.)
As a warm-up, you may consider the same problem but with a known initial state of the switch.
View SolutionSubmit Solution- 1,640.0K views
- 1 answers
- 0 votes
More puzzles to try-

John and Jacob were Friend
One day, John and his friends were playing around. Jacob hit something with a Pin and it popped. John’s dad ...Read More »
Quick and Easy Puzzle
Find the values of a and b: 12 x a + b = 98 123 x a + b+1 = ...Read More »
Open the Door
Two words that can open doors for you for the rest of your life?Read More »
Which is day yesterday
Which day would yesterday be if Thursday was four days before the day after tomorrow?Read More »
Kris Cross
Can you place six X (crosses) in below board without making three in a row in any way ?Read More »
Solve the Equation
Can you solve below mathematical equation? 2^1234 – 2^1233Read More »
Son’s Age
A man asked his neighbour’s son age. He replied in a mathematical way. My son is five times as old ...Read More »
Find the missing amount
Three people check into a hotel. They pay £30 to the manager and go to their room. The manager suddenly ...Read More »
Tricky math fun riddle
What number when divided in half becomes zero ?Read More »
Traveller trapped by king puzzle
A very intelligent and kind Traveller was trapped by a King, King wants to check his intelligence and kindness at ...Read More »
Chomp
Given is a (possibly enormous) rectangular chocolate bar, divided into small squares in the usual way. The chocolate holds a ...Read More »
Father and Son’s Age
The ages of a father and son add up to 66. The father’s age is the son’s age reversed. How ...Read More »
Can\’t touch
You can see it everyday, But cannot touch it at will. What is it ?Read More »
Fariha’s Game
Fariha invented a game! In that game, Fariha kept 5 plates on a circular dining table! The plates were marked ...Read More »
Name The Monkey
Mrs. Robinson’s 4th grade class took a field trip to the local zoo. The day was sunny and warm – ...Read More »
Murder Mystery Riddle
A donkey is behind another donkey I’m behind that second donkey But there is a whole nation behind me It ...Read More »
Two Third Cat
Which city is three-fifths chick two third cat and 50% goat?Read More »
Highest mountain on Earth
Before Mount Everest was discovered, what was the highest mountain on Earth?Read More »
Never resting, never still
Never resting, never still, Moving silently from hill to hill. It does not walk, run or trot, All is cool ...Read More »
Cricket World Cup puzzle
There are 9 team participating in ICC Cricket World Cup, every team will play two matches with every other team. ...Read More »