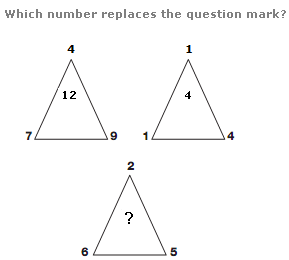
Brain Teasers & Puzzles
-
- 1,621.8K views
- 1 answers
- 1 votes
-
- 1,641.8K views
- 4 answers
- -1 votes
-
Answer the clues below to find each word. Then place the letters on the lines below. Each letter must be placed on a line marked by the same number. When all the lines are full, our Happy New Year greeting will be revealed. 
a greeting .. 
bits of falling shredded paper .. 
to call forth .. 
goals made for the New Year .. 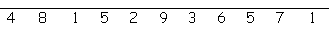
you blow these at festive gatherings .. 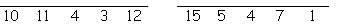
traditional New Year’s song .. 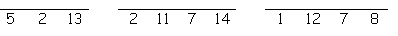
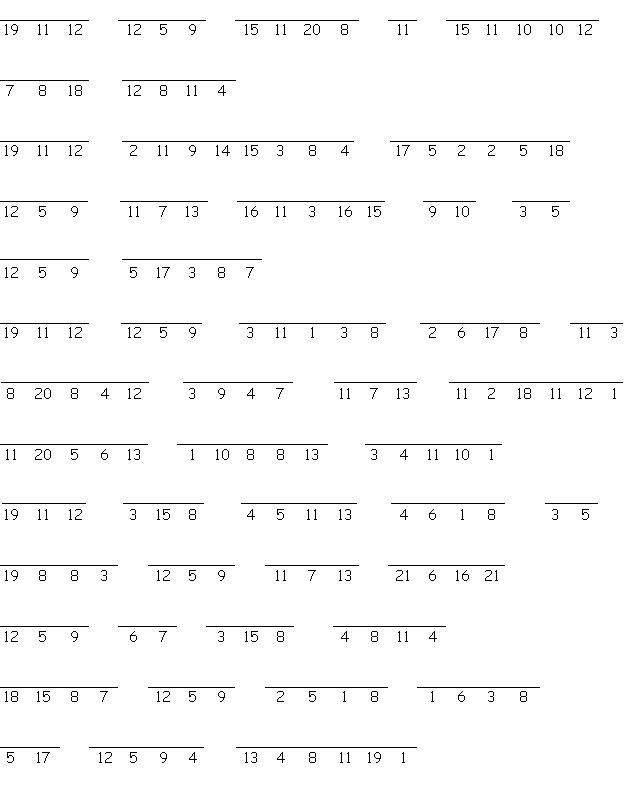 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,614.9K views
- 1 answers
- 0 votes
-
A king has a daughter and wants to choose the man she will marry. There are three suitors from whom to choose, a Knight, a Knave, and a Commoner. The king wants to avoid choosing the Commoner as the bridegroom, but he does not know which man is which. All the king knows is that the Knight always speaks the truth, the Knave always lies, and the Commoner can do either. The king will ask each man one yes/no question, and will then choose who gets to marry the princess. What question should the king ask and how should he choose the bridegroom?
A followup question:
Suppose the three suitors know each other (an assumption that’s not needed in the original problem). Then find a new strategy for the king where the king only needs to ask a question of any two of the three suitors in order to pick the bridegroom.
View SolutionSubmit Solution- 1,620.6K views
- 1 answers
- 0 votes
-
In this problem, you and a partner are to come up with a scheme for communicating the value of a hidden card. The game is played as follows:
- Your partner is sent out of the room.
- A dealer hands you 5 cards from a standard 52 card deck.
- You look at the cards, and hand them back to the dealer, one by one, in whatever order you choose.
- The dealer takes the first card that you hand her and places it, face up, in a spot labeled “0”‘. The next three cards that you hand her, she places, similarly, in spots labeled “1”, “2”, and “3”. The last card that you hand her goes, face down, in a spot labeled “hidden”. (While you control the order of the cards, you have no control over their orientations, sitting in their spots; so you can’t use orientation to transmit information to your partner.)
- Your partner enters the room, looks at the four face-up cards and the spots in which they lie and, from that information (and your previously-agreed-upon game plan), determines the suit and value of the hidden card.
Question: What is the foolproof scheme that you and your partner settled on ahead of time?
As a follow-up question, consider the same problem but with a 124-card deck.
View SolutionSubmit Solution- 1,619.1K views
- 1 answers
- 0 votes
-
You’re an electrician working at a mountain. There are N wires running from one side of the mountain to the other. The problem is that the wires are not labeled, so you just see N wire ends on each side of the mountain. Your job is to match these ends (say, by labeling the two ends of each
wire in the same way).In order to figure out the matching, you can twist together wire ends, thus electrically connecting the wires. You can twist as many wire ends as you want, into as many clusters as you want, at the side of the mountain where you happen to be at the time. You can also untwist the wire ends at the side of the mountain where you’re at. You are equipped with an Ohm meter, which lets you test the connectivity of any pair of wires. (Actually, it’s an abstract Ohm meter, in that it only tells you whether or not two things are connected, not the exact resistance.)
You are not charged [no pun intended] for twisting, untwisting, and using the Ohm meter. You are only charged for each helicopter ride you make from one side of the mountain to the other. What is the best way to match the wires? (Oh, N>2, for there is no solution when N=2.)
View SolutionSubmit Solution- 1,617.2K views
- 1 answers
- 0 votes
-
Given N points randomly distributed around the circumference of a circle, what is the probability that all N points lie on the same semi-circle?
View SolutionSubmit Solution- 1,616.5K views
- 1 answers
- 0 votes
-
In a finite, undirected, connected graph, an integer variable v(n) is associated with each node n. One node is distinguished as the anchor. An operation OP(n) is defined on nodes:
OP(n):
if node n is the anchor, then do nothing,
else set v(n) to the value 1 + min{v(m)}, where m ranges over all neighbors of n that are distinct from n.An infinite sequence of operations <OP(n),OP(m), …> is executed, the node arguments n, m, … for the operations being chosen arbitrarily and not necessarily fairly. Show that eventually all v(n) stabilize. That is, that after some finite prefix of the infinite sequence of operations, no further operation changes v(n) for any node n.
View SolutionSubmit Solution- 1,616.4K views
- 1 answers
- 0 votes
-
A square table has a coin at each corner. Design an execution sequence, each of whose steps consists of one of the following operations:
- ONE: The operation chooses a coin (possibly a different one with each execution of the operation) and flips it.
- SIDE: The operation chooses a side of the table and flips the two coins along that side.
- DIAG: The operation chooses a diagonal of the table and flips the two coins along that diagonal.
such that at some point during the execution (not necessarily at the end), a state where all coins are turned the same way (all heads or all tails) obtains.
View SolutionSubmit Solution- 1,618.8K views
- 2 answers
- 0 votes
-
N prisoners get together to decide on a strategy. Then, each prisoner is taken to his own isolated cell. A prison guard goes to a cell and takes its prisoner to a room where there is a switch. The switch can either be up or down. The prisoner is allowed to inspect the state of the switch and then has the option of flicking the switch. The prisoner is then taken back to his cell. The prison guard repeats this process infinitely often, each time choosing fairly among the prisoners. That is, the prison guard will choose each prisoner infinitely often.
At any time, any prisoner can exclaim “Now, every prisoner has been in the room with the switch”. If, at that time, the statement is correct, all prisoners are set free; if the statement is not correct, all prisoners are immediately executed. What strategy should the prisoners use to ensure their eventual freedom?
(Just in case there’s any confusion: The initial state of the switch is unknown to the prisoners. The state of the switch is changed only by the prisoners.)
As a warm-up, you may consider the same problem but with a known initial state of the switch.
View SolutionSubmit Solution- 1,615.4K views
- 1 answers
- 0 votes
More puzzles to try-

Find the Ladder kept in the Library
Only Highly Attentive Can Spot The Ladder In This Library In 7 Seconds! Can You?Read More »
Long hand of clock
How many times does the long hand of the clock pass the short hand between midnight one day and midnight ...Read More »
Potato
where was the first potato of the world found?Read More »
Stone and Eatable
Tell me the Hindi name of a Vegetable which if we remove 1st word will become a precious Stone and ...Read More »
Count the apples
You have been given the task of transporting 3,000 apples 1,000 miles from Appleland to Bananaville. Your truck can carry ...Read More »
1000 Buildings And Number Of Zeros Puzzles
Fry Link street has 1000 buildings. A sign board maker is contracted to number the houses from 1 to 1000. How ...Read More »
Pet Rabbit riddle
You just bought a cute rabbit at a pet store. The rabbit can breed once every month, and deliver 7 ...Read More »
Nevert Lie
You can see nothing else When you look in his face, He will look you in the eye and He ...Read More »
What is the thing?
What is the thing which, if you have, you cannot marry, and if you don’t have, you can’t have a ...Read More »
Ballon tragedy Riddle
One sunny afternoon, three men go for a ride on a hot air balloon over the Thar desert. After two ...Read More »
Probability of having boy
In a country where everyone wants a boy, each family continues having babies till they have a boy. After some ...Read More »
Oscar-Winning Movie
Can you identify the Oscar-winning movie from the rebus below?Read More »
The Blind Man’s Choice
A blind man was brought to Akbar’s court. Akbar wanted to test Birbal’s intelligence, so he asked Birbal to find ...Read More »
Chance of Winning Lottery
The chance of Mr John winning the lottery is 10%. All participants lined up and Mr John is 4th in ...Read More »
Black and White Hats Puzzle
Naga a safari in the kajiranga jungle capture three men. The naga give the men a single chance to escape uneaten. ...Read More »
week days riddle
How many days in a week start with the letter T?Read More »
Who’s Not Like the Others?
Even in a scientist’s lab, something can be out of place! Find the odd one out in this Frankenstein-themed brain ...Read More »
Multiplication Riddle
Can you find three consecutive odd numbers that gives total 1,287 when multiplied together?Read More »
Rearrange Paper
There is a square piece of paper with a hole that is denoted by the circle on the top right ...Read More »
Rebus World Puzzle
What does this say? ISSUES ISSUES ISSUES ISSUES ISSUES ISSUES ISSUES ISSUES ISSUES ISSUESRead More »