Three hat colors Microsoft Puzzle
A team of three people decide on a strategy for playing the following game. Each player walks into a room. On the way in, a fair coin is tossed for each player, deciding that player’s hat color, either red or blue. Each player can see the hat colors of the other two players, but cannot see her own hat color. After inspecting each other’s hat colors, each player decides on a response, one of: “I have a red hat”, “I had a blue hat”, or “I pass”. The responses are recorded, but the responses are not shared until every player has recorded her response. The team wins if at least one player responds with a color and every color response correctly describes the hat color of the player making the response. In other words, the team loses if either everyone responds with “I pass” or someone responds with a color that is different from her hat color.
What strategy should one use to maximize the team’s expected chance of winning?
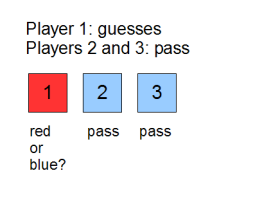
For example, one possible strategy is to single out one of the three players. This player will respond “I have a red hat” and the others will respond “I pass”. The expected chance of winning with this strategy is 50%. Can you do better? Provide a better strategy or prove that no better strategy exists.
I know there is already an extensive answer to this question, but I haven’t read it. Given the length of the existing answer, perhaps my explanation will be simpler.
There is a 25% chance that all hats are the same color and a 75% chance that there are 2 hats of one color and 1 hat of another color. The strategy is to have a player pass unless both the hats they see are the same color. If a player sees two hats of the same color, they respond that their hat is the opposite color. In this manner, the team always wins when there are multiple hat colors (only the person wearing the hat that is different than the other two responds and correctly identifies the color of their hat), and always loses when all the hats are the same color (they all claim their hat is the wrong color).
TO achieve 75 percent chance of winning
Strategy:
Player 1:
If see blue-red, then pick red.
If see red-blue, then pick blue.
Else pass.
Player 2:
If see red-red, then pick blue.
If see blue-blue, then pick red.
Else pass.
Player 3:
If see red-blue, then pick red.
If see blue-red, then pick blue
Else pass.
Very good explanation at – EXPLANATION
EXPLAINATION From mindyourdecision.com –
(In the language of game theory, this is a simultaneous coordination game of incomplete information.)
If the players could talk after they had hats on, the game would be trivial. Since the players have incentive to cooperate, they would honestly reveal what they see. In a matter of seconds, they could all figure out their hat colors and guess correctly.
But the rules only allow for an initial strategy session. How well can the players fare? Amazingly, they can do pretty well.
The Basic Strategy (50 percent winning)
The rules heavily penalize incorrect guesses. A single incorrect guess makes the group lose–even if the other two players guess correctly. A single incorrect guess is the apple that spoils the bunch.
So it’s important the rules allow for players to pass. If a player doesn’t have a good guess, it would be a good idea to pass.
A basic strategy would be to minimize the risk of bad guesses. Force two players to pass in every game and make one person the official guesser. The group wins exactly when this person guesses correctly.
How often will the group succeed? Since the hat color is chosen by a coin flip, there is a 50 percent chance of guessing the correct color.
This is not too shabby when there’s a $3 million dollar reward at stake. I will take that gamble any day.
If I were conducting an interview, I would be satisfied if an applicant, never having heard the puzzle, came this far. The answer demonstrates basic risk management and an understanding of probability.
But can the team do better than random chance?
If you’ve been reading my game theory articles, then you would guess that they can. Players can do often do better than random chance if they consider the distribution of outcomes–a tactic I described in my article about finding true love.
The trick is figuring out the players do have a way of coordinating as a group. Doing this, they can make winning an amazing 75 percent chance. Let’s investigate why.
One Optimal Strategy (75 percent winning)
Motivating question: does observing the other two hat colors tell you anything about your own hat color? In other words, if you see two red hats, does that make your hat more likely to be blue?
The answer is no, and that’s a potential roadblock. Regardless of what you see, your hat color is determined by a coin flip. Fair coins are never “due” for a particular outcome–each toss is independent.
But don’t get caught up in probability–the fact is that seeing the other hat colors does convey information. The problem is the figuring out how to transmit that information to the other players.
To get around that, players need to coordinate guesses based on what they see. If possible, they still want to minimize bad guesses by having two people pass and one person guess. What’s needed now is a group strategy.
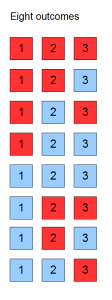
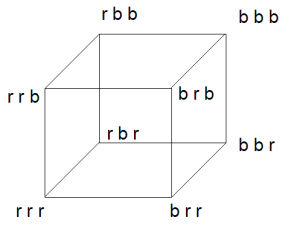
How can they do that? It starts by taking a step back and considering the possible distributions of hat outcomes. With three players and two hat colors, there are a total of eight equally likely outcomes:
Is there anything special about the distribution?
One feature is that most outcomes–six of them–include at least one hat of both colors. Only two extreme outcomes don’t–the ones with all red hats or all blue hats.
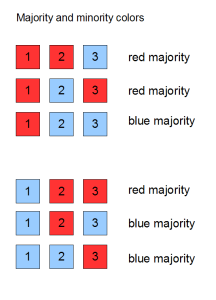
We can analyze further. Among outcomes with both hat colors, there logically has to be two hats of one color (the “majority” color) and one hat of another color (the “minority” color).
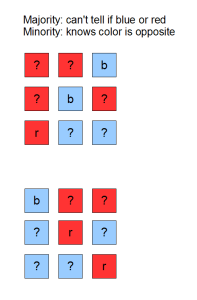
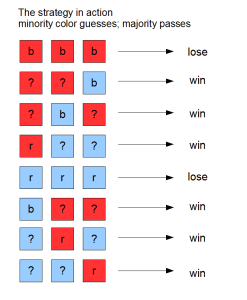
Here’s the kicker: by looking at the other hats, players can identify whether they are wearing a majority color or a minority color.
For instance, if a player sees both a red and blue hat, then the player must be wearing the majority color (which could be red or blue).
If a player sees two blue or two red hats, then the player must be wearing the minority color, which will be the opposite color of what the player sees.
Here is what players can reason among the six choices:
Now the idea is to get the player with the minority hat color to guess and force the other people to pass.
So here is the strategy:
- if you see both a red and a blue hat, then “pass”
- if you see two red hats, then guess “blue”
- if you see two blue hats, then guess “red”
This strategy wins in all six cases with at least one hat of each color. It only loses in the two cases of all-red or all-blue, in which all players guess incorrectly.
Here is how players would guess:
All told, the group wins in six of eight possible outcomes–a whopping 75 percent chance.
Optional Extra Credit: The Host can Learn
If you’re playing rock-paper-scissors against a computer that mixes randomly, you could win 1/3 of the time simply by picking one strategy, say rock. But if the computer could learn and analyze your pattern, it might respond by countering with paper and start winning a lot. To maintain your 1/3 winning chance, you need to randomize your choices among rock, paper, and scissors.
In the hat game, the players have a 75 percent chance of winning, but the strategy has a pattern. It loses every time the hat colors are all the same. A responsive host, like the computer in rock-paper-scissors, would see the pattern and respond by assigning hats to be the all one color more frequently. To keep the host honest, the players need to randomize.
Is there some a way the players can win, without creating a pattern of outcomes in which they all lose?
Amazingly, yes there is! Even more surprising, the winning percentage stays at 75 percent.
In researching this article, I learned about the claim and a proposed winning strategy from a presentation on Michel Waldschmit’s website called “Coding Theory, Card Tricks and Hat Problems.”
Unfortunately the slides didn’t contain the proof, or an example, so I felt a little bit like I was staring at the margin of a textbook from Fermat.
I took out my own pencil and paper and worked on the answer. I am happy to say I came up with the following analysis myself.
The Random Optimal Strategy (75 percent winning)
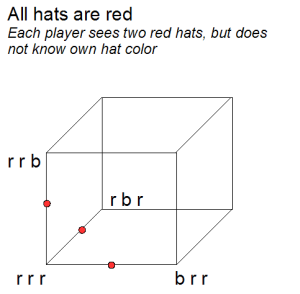
The random strategy is a refinement on the static one given above. The key to the above strategy is that players essentially bet against the outcome being all-red or all-blue. Knowing that, it was possible to coordinate guesses so only one person guessed and gave a correct answer.
There’s nothing special about picking all-red or all-blue.
The players can randomly pick any color combination and its “opposite” configuration (red-blue-red and blue-red-blue are opposites) as outcomes to bet against. The remaining six outcomes can be coded based on the hat colors that each player sees.
Why would this work, and why does it have to be “opposite” combinations?
The eight outcomes of the hat game can be visualized as vertices of a cube. Adjacent vertices differ by changing only a single “coordinate,” that is, the color of one player’s hat.
The graphical interpretation is as follows: can the players identify which vertex they belong to? The information they are given is the other two hat colors they see–that is, they are effectively placed at midway points along the adjacent edges.
Each player can see the coordinates of the other two players, but is unsure about the own coordinate–that is, the player is unsure which of the two possible endpoints the group belongs to.
We want a situation where exactly two players will not be able to tell the vertex (they will “pass”) and the remaining player will know the location (and guess correctly).
Such a unique coding occurs when players bet against a random vertex and the “opposite” one–a limitation that gives maximal location information.
In any of these cases, players only lose if in fact the outcome is one of the two they bet against, meaning they have a 75 percent chance of winning.
The 75 percent chance of winning applies to every time the game is played but the losing outcomes are randomized. Hence, the host won’t be able to exploit any particular color combination.
All the combinations may be as follows-
1 red ,2 blue
2 red,1 blue
3 red
3 blue
so the planning should be that whichever player sees 2 same colored hat on the other two team mates, should go first & respond as “i pass”. & by this the other 2 will get to know that they both have same color hats,so by seeing the color of hat of another one they will get to know the color of their own hate. so the team will always win. ( correct me if my answer has broken a rule of puzzle)

Responses are not shared until every player has recorded the response.
Guys, consider this solution:
Let the players be A, B and C. They make the following strategy.
2R 1R1B 2B
A Red Pass Blue
B Pass Blue Red
C Blue Red Pass
That is, if A sees two red hats (on B and C), he says red. If C sees a red and a blue hat, he says red, and so on.
Now consider the following cases:
1) 3 red hats (A-red, B-red, C-red)
Here, according to the table, A will say red, B will pass and C will say blue. Since A’s answer is correct, they will win.
2) 2 red hats, one blue hat
(a) A-blue, B-red, C-red
A will say red, B will say blue and C will say red. Since C’s answer is correct, they will win.
(b) A-red, B-blue, C-red
A and B will pass, while C will say red. Since C’s answer is correct, they will win once again.
(c) A-red, B-red, C-blue
A will pass, while both B and C will say blue. Since C’s answer is correct, they will win the game.
3) 1 red hat, 2 blue hats
(a) A-red, B-blue, C-blue
A and B will both say blue, while C will say red. Since B’s answer is correct, they will win.
(b) A-blue, B-red, C-blue
A passes, B says red and C also says red. Since B gave the correct answer, they win.
(c) A-blue, B-blue, C-red
A passes, B says blue and C passes. Since B is correct, they win.
4) 3 blue hats (A-blue, B-blue, C-blue)
In this case, A will say blue, B will say red while C will pass. Since A gave the correct answer, they win.
Thus this strategy provides for a 100% hit rate, since they win in every possible case. But every answer to this question, here as well as elsewhere, gives a 75% accuracy. Could someone please point out an error in this strategy?
There is a 75% chance that 2 members will have the same coloured hat.
If there are 2 members with the same coloured hat then pick the opposite colour.
If not someone will have to guess and the other 2 members will have to pass.
Your Answer
More puzzles to try-

What is the logic behind these ?
3 + 3 = 3 5 + 4 = 4 1 + 0 = 3 2 + 3 = 4 ...Read More »
Defective stack of coins puzzle
There are 10 stacks of 10 coins each. Each coin weights 10 gms. However, one stack of coins is defective ...Read More »
Which clock works best?
Which clock works best? The one that loses a minute a day or the one that doesn’t work at all?Read More »
(Advanced) Cheryl’s Birthday Puzzle
Paul, Sam and Dean are assigned the task of figuring out two numbers. They get the following information: Both numbers ...Read More »
Five greedy pirates and gold coin distribution Puzzle
Five puzzleFry ship’s pirates have obtained 100 gold coins and have to divide up the loot. The pirates are all ...Read More »
Magical flowers!!
A devotee goes to three temples, temple1, temple2 and temple3 one after the other. In front of each temple, there ...Read More »
Tuesday, Thursday what are other two days staring with T?
Four days are there which start with the letter ‘T‘. I can remember only two of them as “Tuesday , Thursday”. ...Read More »
How could only 3 apples left
Two fathers took their sons to a fruit stall. Each man and son bought an apple, But when they returned ...Read More »
How Many Eggs ?
A farmer is taking her eggs to the market in a cart, but she hits a pothole, which knocks over ...Read More »
HARD MATHS – How much faster is one train from other Puzzle
Two trains starting at same time, one from Bangalore to Mysore and other in opposite direction arrive at their destination ...Read More »
Most Analytical GOOGLE INTERVIEW Question Revealed
Let it be simple and as direct as possible. Interviewer : Tell me how much time (in days) and money would ...Read More »
Lateral thinking sequence Puzzle
Solve this logic sequence puzzle by the correct digit- 8080 = 6 1357 = 0 2022 = 1 1999 = ...Read More »
How did he know?
A man leaves his house in the morning to go to office and kisses his wife. In the evening on ...Read More »
Pizza Cost Math Brain Teaser
Jasmine, Thibault, and Noah were having a night out and decided to order a pizza for $10. It turned out ...Read More »
Which letter replaces the question mark
Which letter replaces the question markRead More »
Which room is safest puzzle
A murderer is condemned to death. He has to choose between three rooms. The first is full of raging fires, ...Read More »
Richie’s Number System
Richie established a very strange number system. According to her claim for different combination of 0 and 2 you will ...Read More »
Srabon wanted to pass
The result of math class test came out. Fariha’s mark was an even number. Srabon got a prime!! Nabila got ...Read More »
Become Normal!!
Robi is a very serious student. On the first day of this year his seriousness for study was 1 hour. ...Read More »
Sakib Knows The Number!
Ragib: I got digits of a 2 digit number Sakib: Is it an odd? Ragib: Yes. Moreover, the sum of ...Read More »