Logic Puzzles
The Latest and exclusive collection of Logic Puzzles to tease your brain. Logic Puzzles helps exercising the brain and develop it to think logical and solve real world problems differenlty. PuzzleFry brings you the best Logic Puzzles, you'll enjoy wide range of Logic Puzzles, Lets try few Logic Puzzles listed below -
-
Man Wrinkle spent one-fourth of his life as a boy, one-eighth as a youth, and one-half as an active man. If Man Wrinkle spent 11 years as an old man,
Then how many years did he spend as an active man?
 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,338.8K views
- 2 answers
- 0 votes
-
If a peacock and a half, lay an egg and a half, in a day and a half.
How many eggs can a peacock lay in three days?PS:- Use logic
 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,341.4K views
- 3 answers
- 0 votes
-
What should be the missing number
3 11 18
33 29 ?
36 38 39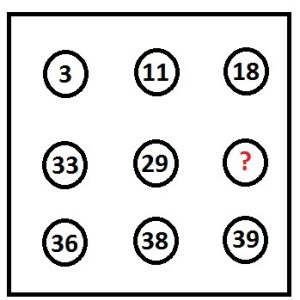 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,345.3K views
- 1 answers
- 0 votes