Brain Teasers & Puzzles
-
There are 100 doors, all closed. In a nearby cage are 100 monkeys. The first monkey is let out, and runs along the doors opening every one. The second monkey is then let out, and runs along the doors closing the 2nd, 4th, 6th,… all the even-numbered doors. The third monkey is let out. He attends only to the 3rd, 6th, 9th,… doors (every third door, in other words), closing any that is open and opening any that is closed, and so on. After all 100 monkeys have done their work in this way, what state are the doors in after the last pass, which doors are left open and which are closed ?
View SolutionSubmit Solution- 1,634.4K views
- 1 answers
- 0 votes
-
This year on October 2, 2001, the date in MMDDYYYY format will be a palindrome (same forwards as backwards).
10/02/2001
When was the last date that this occurred on?View SolutionSubmit Solution- 1,633.7K views
- 1 answers
- 0 votes
-
You have a normal six sided cube. I give you six different colors that you can paint each side of the cube with (one color to each side). How many different cubes can you make?Different means that the cubes can not be rotated so that they look the same. This is important! If you give me two cubes and i can rotate them so that they appear identical in color, they are the same cube.
View SolutionSubmit Solution- 1,634.7K views
- 1 answers
- 0 votes
-

One fine day, Mr. Puzzle and Mr. Fry were playing cards, but suddenly power went off and they were getting bored. So Mr. Puzzle randomly inverted position of 15 cards out of 52 cards(and shuffled it) and asked Mr. Fry to divide the card in two pile with equal number of inverted cards(number of cards in each pile need not be equal).
It was very dark in the room and Mr. Fry could not see the cards, after thinking a bit Mr. Fry divided the cards in two piles and quite surprisingly on counting number of inverted cards in both the piles were equal.
What do you think Mr. Fry must have done?
View SolutionSubmit Solution- 1,670.1K views
- 5 answers
- 2 votes
-
- 1,636.3K views
- 2 answers
- 0 votes
-
First of all, I would redefine the concept of thegreen synthesis, because I don’t want to reducethis to an obvious statement and swear thatblack is white
View SolutionSubmit Solution- 1,637.2K views
- 2 answers
- 0 votes
-
Also known as Hempel’s Paradox, for the German logician who proposed it in the mid-1940s, the Raven Paradox begins with the apparently straightforward and entirely true statement that “all ravens are black.”
The paradox here is that Hempel has apparently proved that seeing an apple provides us with evidence, no matter how unrelated it may seem, that ravens are black. It’s the equivalent of saying that you live in New York is evidence that you don’t live in L.A., or that saying you are 30 years old is evidence that you are not 29. Just how much information can one statement actually imply anyway?
View SolutionSubmit Solution- 1,636.9K views
- 1 answers
- 0 votes
-
Imagine that a farmer has a sack containing 100 lbs of potatoes. The potatoes, he discovers, are comprised of 99% water and 1% solids, so he leaves them in the heat of the sun for a day to let the amount of water in them reduce to 98%. But when he returns to them the day after, he finds his 100 lb sack now weighs just 50 lbs. How can this be true? Well, if 99% of 100 lbs of potatoes is water then the water must weigh 99 lbs. The 1% of solids must ultimately weigh just 1 lb, giving a ratio of solids to liquids of 1:99. But if the potatoes are allowed to dehydrate to 98% water, the solids must now account for 2% of the weight—a ratio of 2:98, or 1:49—even though the solids must still only weigh 1lb. The water, ultimately, must now weigh 49lb, giving a total weight of 50lbs despite just a 1% reduction in water content. Or must it?
Although not a true paradox in the strictest sense, the counterintuitive Potato Paradox is a famous example of what is known as a veridical paradox, in which a basic theory is taken to a logical but apparently absurd conclusion.
View SolutionSubmit Solution- 1,638.7K views
- 1 answers
- 0 votes
-
In his final written work, Discourses and Mathematical Demonstrations Relating to Two New Sciences (1638), the legendary Italian polymath Galileo Galilei proposed a mathematical paradox based on the relationships between different sets of numbers. On the one hand, he proposed, there are square numbers—like 1, 4, 9, 16, 25, 36, and so on. On the other, there are those numbers that are not squares—like 2, 3, 5, 6, 7, 8, 10, and so on. Put these two groups together, and surely there have to be more numbers in general than there are justsquare numbers—or, to put it another way, the total number of square numbers must be less than the total number of square and non-square numbers together. However, because every positive number has to have a corresponding square and every square number has to have a positive number as its square root, there cannot possibly be more of one than the other.
Confused? You’re not the only one. In his discussion of his paradox, Galileo was left with no alternative than to conclude that numerical concepts like more, less, or fewer can only be applied to finite sets of numbers, and as there are an infinite number of square and non-square numbers, these concepts simply cannot be used in this context.
View SolutionSubmit Solution- 1,637.1K views
- 1 answers
- 1 votes
-
Imagine a fletcher (i.e. an arrow-maker) has fired one of his arrows into the air. For the arrow to be considered to be moving, it has to be continually repositioning itself from the place where it is now to any place where it currently isn’t. The Fletcher’s Paradox, however, states that throughout its trajectory the arrow is actually not moving at all. At any given instant of no real duration (in other words, a snapshot in time) during its flight, the arrow cannot move to somewhere it isn’t because there isn’t time for it to do so. And it can’t move to where it is now, because it’s already there. So, for that instant in time, the arrow must be stationary. But because all time is comprised entirely of instants—in every one of which the arrow must also be stationary—then the arrow must in fact be stationary the entire time. Except, of course, it isn’t.
View SolutionSubmit Solution- 1,637.6K views
- 1 answers
- 1 votes
-
To solve the puzzle read the riddle and answer the clues below to find each word. Then place the letters on the lines below. Each letter must be placed on a line marked by the same number. When all the lines are full, the answer to the riddle is revealed. Riddle: What do you get from a pampered cow?

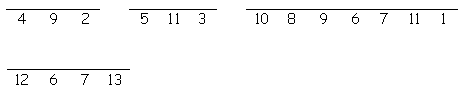
 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,635.5K views
- 1 answers
- 0 votes
-
Find a 4-letter word for each blank below so that when added, two new words (sharing the same middle word) are created. What is each word?
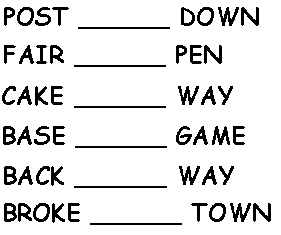 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,633.9K views
- 1 answers
- 0 votes
-
Here’s a Sudoku challenge with a different spin. Instead of using numbers, the puzzle is made with letters! Can you solve the puzzle so that each of the nine letters are present in each 9×9 grid only once, and also each letter only appears once in each column and row?
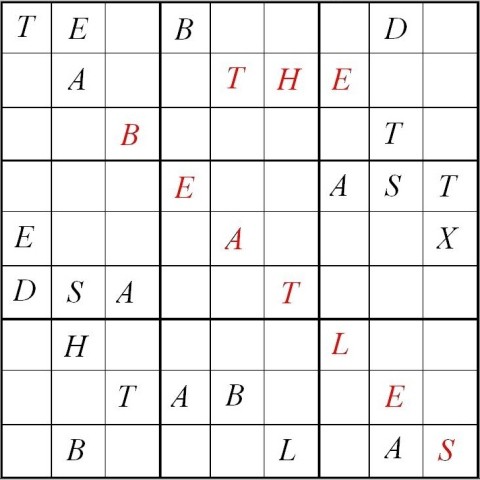 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,635.7K views
- 1 answers
- 0 votes
-
Dorry the Dragon just can’t help himself….he loves beach balls! Unfortunately, beach balls don’t like him much – they tend to pop and loose air. Then they’re not much fun at all. So, can you help Daryl resist his beach ball frenzy? Draw five straight lines through the box below to separate Daryl from the beach balls. When all the lines have been drawn, each section containing Daryl can’t have beach balls in it too.
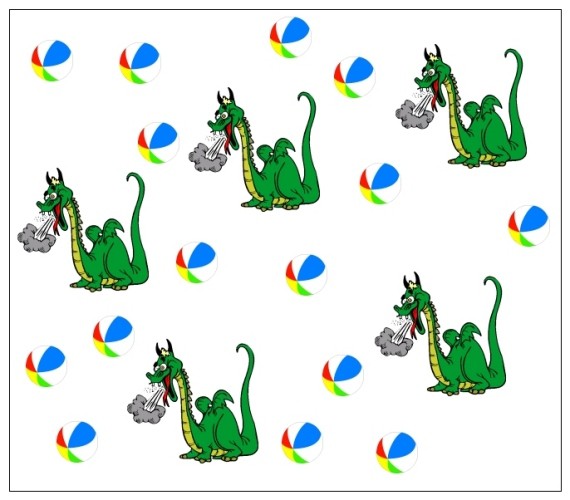 View SolutionSubmit Solution
View SolutionSubmit Solution- 1,633.6K views
- 1 answers
- 0 votes
-
Five friends from across the United States planned to meet at a convention in Milwaukee. Each friend came from a different city and each was employed in a different profession. Use the clues to determine the full name of each friend, their home city, and each one’s profession.
- The doctor and Mr. Cross both arrived a day early.
- By coincidence, the secretary from San Diego and the doctor, Ms. Forest, arrived at the hotel together.
- The lawyer arrived late. He was delayed by a case and had to catch a later flight from Baltimore.
- Jane, Mr. Smith, Mark, the mechanic, and the friend from Chicago all planned to spend the weekend after the convention together. Then on Monday, Ms. Trent and Tom would leave to return to work. Dan, the teacher, and Cindy would leave on Tuesday.
- Dan Richards does not live in Baltimore. Cindy does not live in St. Louis.
- Ms. Trent laughed when asked if she was a teacher. “No, he’s from Atlanta,” she said. “I’m from San Diego.”
View SolutionSubmit Solution- 1,634.5K views
- 1 answers
- 0 votes
More puzzles to try-

Earth and Heaven riddle
Scientists are trying to find out what is between earth and heaven. Can you find me?Read More »
Work with different statement riddle
Three working females have different type of work. If only one of statements 1, 2 and 3 are true, can ...Read More »
Next number in this sequence: 1, 11, 21, 1211, 111221, 312211, 13112221?
What is the next number in this sequence: 1, 11, 21, 1211, 111221, 312211, 13112221, _________?Read More »
A Man and a Dog
A man and a dog were going down the street. The man rode, yet walked. What was the dog’s name?Read More »
The Coal, Carrot and Scarf
Five pieces of coal, a carrot and a scarf are lying on the lawn. Nobody put them on the lawn ...Read More »
White Box without Key Puzzle
I am a white box having no key or lid. Yet there is a golden treasure inside it. What Am ...Read More »
The cream is heavier than the Milk
The cream is heavier than Milk. True or False?Read More »
Olympic Play riddle
At last month’s rehearsal, four top athletes competed in two qualifying 200 meter races. As the results were expected to ...Read More »
Lying World war story riddle
Two friends Smith and Andrew were talking about bravery of their families. Smith told great stories about his courageous grandfather ...Read More »
Logical Algebra
Solve the equation by replacing the alphabet with numbers. MOM + MOM + NO = BOOK=Read More »
Today I am gone
Tomorrow I am surely here, yesterday I am found as well. Today I am gone. Who am I?Read More »
What time will the dish be full?
A Petri dish hosts a healthy colony of bacteria. Once a minute every bacterium divides into two. The colony was ...Read More »
Chinese Checkers Puzzle
See the given image carefully. What you have to do is move the blue checkers in the position of the ...Read More »
Found underground riddle
These are a type of starchy food Mashed or fried they can be found They often come from Idaho And ...Read More »
A simple probability question
Mr. Smith has two children. If the older child is a boy, what are the odds that the other child ...Read More »
How many people have guessed three fruits correctly, and how many people have guessed four fruits correctly?
In a contest, four fruits (an apple, a banana, an orange, and a pear) have been placed in four closed ...Read More »
Maximum run in cricket puzzle
In a one day cricket match, There were no wide balls, no wides, no extras and no overthrows. What is ...Read More »
Crazy horse puzzle
A horse jumps over a castle and lands on a man, then the man disappears. How was this possible?Read More »
100 Chocolates
Joseph buys three kinds of chocolates for 100 rupees. The first one is priced at 5 rupees, second one at ...Read More »
Dogs and Food Riddle
During a recent research project, again with the JD associates, leading experts determined that three-legged dogs eat less food than ...Read More »



