train and Bridge riddle
John walks over a railway-bridge. At the moment that he is just ten meters away from the middle of the bridge, he hears a train coming from behind. At that moment, the train, which travels at a speed of 90 km/h, is exactly as far away from the bridge as the bridge measures in length. Without hesitation, John rushes straight towards the train to get off the bridge. In this way, he misses the train by just four meters! If John had rushed exactly as fast in the other direction, the train would have hit him eight meters before the end of the bridge.
What is the length of the railway-bridge? 
we konw ,
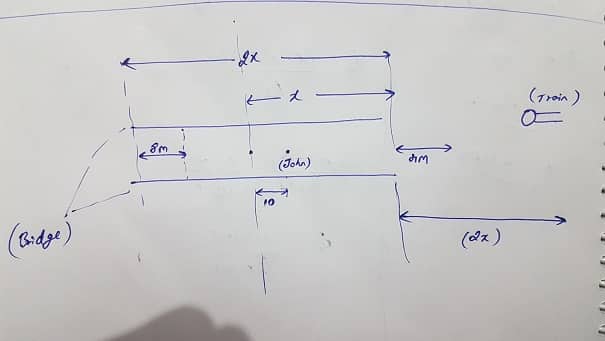
speed = distance/time & length of bridge = 2x
If john runs back , he misses the train by just 4 meters that means ,
that means (time taken by john to reach the right end of bridge) = (time taken by the train to reach 4meters before the start of bridge)
speed (train) = 90kmph = (2x – 4)/t & speed (john) = (x-10)/t {refer the above diagram}
t = (2x-4)/90 = (x-10)/speed(john) ………………………………(1)
similarly,
if john runs to the left of the bridge the train hits him 8 meters before the end so,
(time taken by the train to reach 8 meters before left end of the bridge ) = time taken by john to reach 8 meters before the left end of the bridge)
speed(train) = 90 = (2x + 2x -8)/t* & speed(john) = (x -8 + 10) / t*
t* = (4x-8)/90 = (x+2)/speed(john)
so,
speed(john) = (x+2)/(4x-8)(90) ……………………………………………(2)
substitute(2) in equation (1)…..
you get the answer.
NOTE: (The units does not matter as it is going to get cancelled from both RHS and LHS)
I think you did wrong
tell me where have i gone wrong..i’ll try to rectify..
units are not dealt with properly in calculation I think km/h and meters
I also got the answer 44:
Bridge is B meter long
starting position John: B/2-10
starting position train: -B
situation 1: Running back
the train traveled B-4 meter
time it took: (B-4)/vt
John traveled B/2-10 meter in the same time
John’s speed vj = vt*(B/2-10)/(B-4)
situation 2: running forward
the train traveled 2B-8 (=2*(B-4)) meter
time it took: (2B-8)/vt
John traveled (B-8) – (B/2-10) = B/2+2 meter in the same time
John’s speed vj = vt*(B/2+2)/(2B-8)
vt*(B/2-10)/(B-4) = vt*(B/2+2)/(2B-8)
(B/2-10) = (B/2+2)/2
2B-40 = B+4
B = 44
vj=vt*0,3 = 27 km/h (about 17 mi/h)
all units used are meters.
The speed isn’t used at all so its units aren’t relevant
Your Answer
More puzzles to try-

What is the logic behind these ?
3 + 3 = 3 5 + 4 = 4 1 + 0 = 3 2 + 3 = 4 ...Read More »
Defective stack of coins puzzle
There are 10 stacks of 10 coins each. Each coin weights 10 gms. However, one stack of coins is defective ...Read More »
Which clock works best?
Which clock works best? The one that loses a minute a day or the one that doesn’t work at all?Read More »
(Advanced) Cheryl’s Birthday Puzzle
Paul, Sam and Dean are assigned the task of figuring out two numbers. They get the following information: Both numbers ...Read More »
Five greedy pirates and gold coin distribution Puzzle
Five puzzleFry ship’s pirates have obtained 100 gold coins and have to divide up the loot. The pirates are all ...Read More »
Magical flowers!!
A devotee goes to three temples, temple1, temple2 and temple3 one after the other. In front of each temple, there ...Read More »
Tuesday, Thursday what are other two days staring with T?
Four days are there which start with the letter ‘T‘. I can remember only two of them as “Tuesday , Thursday”. ...Read More »
How could only 3 apples left
Two fathers took their sons to a fruit stall. Each man and son bought an apple, But when they returned ...Read More »
How Many Eggs ?
A farmer is taking her eggs to the market in a cart, but she hits a pothole, which knocks over ...Read More »
HARD MATHS – How much faster is one train from other Puzzle
Two trains starting at same time, one from Bangalore to Mysore and other in opposite direction arrive at their destination ...Read More »
Most Analytical GOOGLE INTERVIEW Question Revealed
Let it be simple and as direct as possible. Interviewer : Tell me how much time (in days) and money would ...Read More »
Lateral thinking sequence Puzzle
Solve this logic sequence puzzle by the correct digit- 8080 = 6 1357 = 0 2022 = 1 1999 = ...Read More »
How did he know?
A man leaves his house in the morning to go to office and kisses his wife. In the evening on ...Read More »
Pizza Cost Math Brain Teaser
Jasmine, Thibault, and Noah were having a night out and decided to order a pizza for $10. It turned out ...Read More »
Which letter replaces the question mark
Which letter replaces the question markRead More »
Which room is safest puzzle
A murderer is condemned to death. He has to choose between three rooms. The first is full of raging fires, ...Read More »
Richie’s Number System
Richie established a very strange number system. According to her claim for different combination of 0 and 2 you will ...Read More »
Srabon wanted to pass
The result of math class test came out. Fariha’s mark was an even number. Srabon got a prime!! Nabila got ...Read More »
Become Normal!!
Robi is a very serious student. On the first day of this year his seriousness for study was 1 hour. ...Read More »
Sakib Knows The Number!
Ragib: I got digits of a 2 digit number Sakib: Is it an odd? Ragib: Yes. Moreover, the sum of ...Read More »