Brain Teasers & Puzzles
-
Given the size of the chess board and initial position of the knight, what is the probability that after k moves the knight will be inside the chess board.
Note:-
1) The knight makes its all 8 possible moves with equal probability.
2) Once the knight is outside the chess board it cannot come back inside.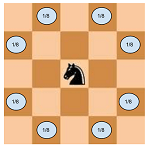
Puzzlefry added Info-
This challenge is originally from a blog post of crazyforcode.com published under the CC BY-NC-ND 2.5 IN licence.View SolutionSubmit Solution- 1,638.1K views
- 2 answers
- 1 votes
-
Imagine that you’re about to set off walking down a street. To reach the other end, you’d first have to walk half way there. And to walk half way there, you’d first have to walk a quarter of the way there. And to walk a quarter of the way there, you’d first have to walk an eighth of the way there. And before that a sixteenth of the way there, and then a thirty-second of the way there, a sixty-fourth of the way there, and so on.
Ultimately, in order to perform even the simplest of tasks like walking down a street, you’d have to perform an infinite number of smaller tasks—something that, by definition, is utterly impossible. Not only that, but no matter how small the first part of the journey is said to be, it can always be halved to create another task; the only way in which it cannot be halved would be to consider the first part of the journey to be of absolutely no distance whatsoever, and in order to complete the task of moving no distance whatsoever, you can’t even start your journey in the first place.
View SolutionSubmit Solution- 1,636.0K views
- 1 answers
- 0 votes
-
One person has some money in his pocket, He visits four temple on the way. As soon as he enters a temple, his money gets double and he offers Rs. 100 in each temple thus his pocket gets empty after he returns from the fourth temple. Now the question is how much money he had initially ?
View SolutionSubmit Solution- 1,637.9K views
- 1 answers
- 1 votes
-
A crocodile snatches a young boy from a riverbank. His mother pleads with the crocodile to return him, to which the crocodile replies that he will only return the boy safely if the mother can guess correctly whether or not he will indeed return the boy. There is no problem if the mother guesses that the crocodile will return him—if she is right, he is returned; if she is wrong, the crocodile keeps him. If she answers that the crocodile will not return him, however, we end up with a paradox: if she is right and the crocodile never intended to return her child, then the crocodile has to return him, but in doing so breaks his word and contradicts the mother’s answer. On the other hand, if she is wrong and the crocodile actually did intend to return the boy, the crocodile must then keep him even though he intended not to, thereby also breaking his word.
The Crocodile Paradox is such an ancient and enduring logic problem that in the Middle Ages the word “crocodilite” came to be used to refer to any similarly brain-twisting dilemma where you admit something that is later used against you, while “crocodility” is an equally ancient word for captious or fallacious reasoning
View SolutionSubmit Solution- 1,638.5K views
- 1 answers
- 0 votes
-
Imagine you’re holding a postcard in your hand, on one side of which is written, “The statement on the other side of this card is true.” We’ll call that Statement A. Turn the card over, and the opposite side reads, “The statement on the other side of this card is false” (Statement B). Trying to assign any truth to either Statement A or B, however, leads to a paradox: if A is true then B must be as well, but for B to be true, A has to be false. Oppositely, if A is false then B must be false too, which must ultimately make A true.
Invented by the British logician Philip Jourdain in the early 1900s, the Card Paradox is a simple variation of what is known as a “liar paradox,” in which assigning truth values to statements that purport to be either true or false produces a contradiction. An even more complicated variation of a liar paradox is the next entry on our list.
Submit Solution- 1,637.2K views
- 0 answers
- -1 votes
-
Imagine that a family has two children, one of whom we know to be a boy. What then is the probability that the other child is a boy? The obvious answer is to say that the probability is 1/2—after all, the other child can only be either a boy or a girl, and the chances of a baby being born a boy or a girl are (essentially) equal. In a two-child family, however, there are actually four possible combinations of children: two boys (MM), two girls (FF), an older boy and a younger girl (MF), and an older girl and a younger boy (FM). We already know that one of the children is a boy, meaning we can eliminate the combination FF, but that leaves us with three equally possible combinations of children in which at least one is a boy—namely MM, MF, and FM. This means that the probability that the other child is a boy—MM—must be 1/3, not 1/2.
View SolutionSubmit Solution- 1,637.4K views
- 1 answers
- 0 votes
-
Mary has 4 sisters…..
Perry, Berry,Terry guess the fourth sisters name?HINT: Its rhythmic with Perry, Berry, Terry
View SolutionSubmit Solution- 1,634.9K views
- 2 answers
- 0 votes
-
Monday Tuesday and Wednesday are three sisters.
What’s their father’s name?
View SolutionSubmit Solution- 1,636.2K views
- 1 answers
- 0 votes
-
- 1,636.6K views
- 1 answers
- 0 votes
-
A man fell in a 30 meter deep well, in one day he climbs 4 meters up and slips 3 meters down. How many days would it take for him to come out of the well?
View SolutionSubmit Solution- 1,682.3K views
- 4 answers
- 1 votes
-
- 1,638.6K views
- 1 answers
- 0 votes
-
A driver, driving a black car with no headlights inside a black tunnel, and he doesn’t meet with an accident. How is it possible?
View SolutionSubmit Solution- 1,637.4K views
- 1 answers
- 2 votes
-
The Bootstrap Paradox is a paradox of time travel that questions how something that is taken from the future and placed in the past could ever come into being in the first place. It’s a common trope used by science fiction writers and has inspired plotlines in everything fromDoctor Who to the Bill and Ted movies, but one of the most memorable and straightforward examples—by Professor David Toomey of the University of Massachusetts and used in his book The New Time Travellers—involves an author and his manuscript.
Imagine that a time traveller buys a copy of Hamlet from a bookstore, travels back in time to Elizabethan London, and hands the book to Shakespeare, who then copies it out and claims it as his own work. Over the centuries that follow, Hamlet is reprinted and reproduced countless times until finally a copy of it ends up back in the same original bookstore, where the time traveller finds it, buys it, and takes it back to Shakespeare. Who, then, wrote Hamlet?
View SolutionSubmit Solution- 1,637.1K views
- 1 answers
- 0 votes
-
The Paradox of Achilles and the Tortoise is one of a number of theoretical discussions of movement put forward by the Greek philosopher Zeno of Elea in the 5th century BC. It begins with the great hero Achilles challenging a tortoise to a footrace. To keep things fair, he agrees to give the tortoise a head start of, say, 500m. When the race begins, Achilles unsurprisingly starts running at a speed much faster than the tortoise, so that by the time he has reached the 500m mark, the tortoise has only walked 50m further than him. But by the time Achilles has reached the 550m mark, the tortoise has walked another 5m. And by the time he has reached the 555m mark, the tortoise has walked another 0.5m, then 0.25m, then 0.125m, and so on. This process continues again and again over an infinite series of smaller and smaller distances, with the tortoise always moving forwards while Achilles always plays catch up.
Logically, this seems to prove that Achilles can never overtake the tortoise—whenever he reaches somewhere the tortoise has been, he will always have some distance still left to go no matter how small it might be. Except, of course, we know intuitively that he can overtake the tortoise. The trick here is not to think of Zeno’s Achilles Paradox in terms of distances and races, but rather as an example of how any finite value can always be divided an infinite number of times, no matter how small its divisions might become.
View SolutionSubmit Solution- 1,637.2K views
- 1 answers
- 0 votes
-
5+5+5=550, use a straight line to prove the equation.
View SolutionSubmit Solution- 1,634.7K views
- 1 answers
- 0 votes
More puzzles to try-

You do everyday
Spelled forwards it is what you do everyday, Spelled backwards it is something you hate. What is it?Read More »
Disney land Racing Puzzle
Doremon organized a race in which Schinchen, jerry, Oggy, and Nobita have participated. The results of the race is as ...Read More »
But it remains
I have one, you have one. Take away a letter and a bit remains. If you remove the second, bit ...Read More »
Find the Unique Number
Can you find the least possible number such that If the number is divided by 3, it gives the remainder ...Read More »
Game of Chess
In the Chess Board picture below white army is arranged. You need to add a black army on the board ...Read More »
Connecting 9 dots with 4 line puzzle
Look at the 9 dots in this image. Can you draw 4 straight lines, without picking up your pen, that ...Read More »
In the Forest
The king’s only children, Abel, Benjamin and Paula, went into the forest with their friend, the elderly Sir Kay. They ...Read More »
Make The King
What king can you make if you take the head of a lamb the middle of a pig the hind ...Read More »
Around the equator
Two identical trains, at the equator start travelling round the world in opposite directions. They start to-gether, run at the ...Read More »
When the planes meet?
There are two planes. One is going from New York to London at a speed of 600 MPH. The other ...Read More »
Prescribed medicine puzzle
A person was prescribed to take two pills (tablets), one each, from the two bottles viz. Bottle A and Bottle ...Read More »
Mechanical Computer riddle
The Puzzlefry mechanical computer is a very sensitive device, it consists of interlocked toothed gear cogs. The largest Cog has ...Read More »
IAS Tricky Riddle
How can a man go eight days without sleep ?Read More »
How many people were at the party?
At a party, everyone shook hands with everybody else. There were 66 handshakes. How many people were at the party?Read More »
Pigs count Cows
A farmer has twenty Goat, ten pigs and ten cows. If we call the pigs cows, how many cows will ...Read More »
Birbal and Real King
The King of a distant land had heard that Birbal was one of the wisest men in the East and ...Read More »
Floors Puzzle
We live in a large tower block, 10 floors high. My 5 year old son goes to school each day ...Read More »
Fire & Air ridle
Jacob is hanging out on a heavily forested island that is really narrow: it is a narrow strip of land ...Read More »
He is found on ground
He is not found on any ground, But always in the air; Though charged each cloud with thunder loud, You ...Read More »
Who Reach The Destination First
John and Jacob are planning on a vacation. John says, “It will be better if we take the train to ...Read More »


